练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某超市举办酬宾活动，单次购物超过元的顾客可参与一次抽奖活动，活动规则如下：盒子中装有大小和形状完全相同的个小球，其中个红球、个白球和个黑球，从中不放回地随机抽取个球，每个球被抽到的机会均等.每抽到个红球记分，每抽到个白球记分，每抽到个黑球记分.如果抽取个球总得分分可获得元现金，总得分低于分没有现金，其余得分可获得元现金.

    （1）设抽取个球总得分为随机变量，求随机变量的分布列；

    （2）设每位顾客一次抽奖获得现金元，求的数学期望.

    【答案】（1）分布列见解析；（2）

    【解析】

    （1）由题意的可能得分为，分别求出相应的概率，由此能求出随机变量的分布列.

    （2）由题意得的可能取值为，分别求出相应的概率，由此能求的数学期望.

    （1）随机变量的所有可能取值为，，，，.

    ，，，

    ，.

    随机变量的分布列为

    （2）由（1）知

    .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

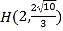    【题目】已知椭圆的右焦点为，点在椭圆上．

    （Ⅰ）求椭圆的方程；

    （Ⅱ）点在圆上，且在第一象限，过作的切线交椭圆于两点，问： 的周长是否为定值？若是，求出定值；若不是，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市垃圾处理厂的垃圾年处理量（单位：千万吨）与资金投入量x（单位：千万元）有如下统计数据：

    2012年

    2013年

    2014年

    2015年

    2016年

    资金投入量x（千万元）

    1.5

    1.4

    1.9

    1.6

    2.1

    垃圾处理量y（千万吨）

    7.4

    7.0

    9.2

    7.9

    10.0

    （1）若从统计的5年中任取2年，求这2年的垃圾处理量至少有一年不低于8.0（千万吨）的概率；

    （2）由表中数据求得线性回归方程为，该垃圾处理厂计划2017年的垃圾处理量不低于9.0千万吨，现由垃圾处理厂决策部门获悉2017年的资金投入量约为1.8千万元，请你预测2017年能否完成垃圾处理任务，若不能，缺口约为多少千万吨？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校从学生会宣传部6名成员(其中男生4人，女生2人)中，任选3人参加某省举办的“我看中国改革开放三十年”演讲比赛活动．

    (1)设所选3人中女生人数为ξ，求ξ的分布列；

    (2)求男生甲或女生乙被选中的概率；

    (3)设“男生甲被选中”为事件A，“女生乙被选中”为事件B，求P(B)和P(B|A)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某车站每天上午发出两班客车，每班客车发车时刻和发车概率如下：第一班车：在8:00，8:20，8:40发车的概率分别为，，；第二班车：在9:00，9:20，9:40发车的概率分别为，，．两班车发车时刻是相互独立的，一位旅客8:10到达车站乘车．求：

    （1）该旅客乘第一班车的概率；

    （2）该旅客候车时间（单位：分钟）的分布列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】经过点P(3,2),且在两坐标轴上的截距相等的直线方程为（写出一般式）___．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列的前项和为，且满足，，设，则以下四个命题：（1）是等差数列；（2）中最大项是；（3）通项公式是；（4）.其中真命题的序号是______.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）当时，求函数的单调区间；

    （2）若不等式对任意的正实数都成立，求实数的最大整数值.

    （3）当时，若存在实数且，使得，求证.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直角梯形中，，，，，是的中点，是与的交点．将沿折起到的位置，如图．

    （Ⅰ）证明：平面；

    （Ⅱ）若平面平面，求平面与平面夹角的余弦值．

    查看答案和解析>>

    同步练习册答案