
 如图,已知瞭望塔BA的高度为40m,为测得古塔DC的高度,在B处望占塔的顶部,仰角是60°,在A处再次望古塔的顶部,仰角为45°.
如图,已知瞭望塔BA的高度为40m,为测得古塔DC的高度,在B处望占塔的顶部,仰角是60°,在A处再次望古塔的顶部,仰角为45°.分析 (1)利用正切函数,即可得出结论;
(2)利用和角的正切函数,即可得出结论.
解答 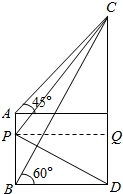 解:(1)设BD=xm,则CD=$\sqrt{3}$x,
解:(1)设BD=xm,则CD=$\sqrt{3}$x,
∴$\sqrt{3}$x-x=40,
∴x=$\frac{40}{\sqrt{3}-1}$=20($\sqrt{3}$+1),
∴CD=20(3+$\sqrt{3}$)m;
(2)设BP=am,则tan∠CPQ=$\frac{20(3+\sqrt{3})-a}{20(\sqrt{3}+1)}$,tan∠DPQ=$\frac{a}{20(\sqrt{3}+1)}$,
∴tan∠CPD=$\frac{\frac{20(3+\sqrt{3})-a}{20(\sqrt{3}+1)}+\frac{a}{20(\sqrt{3}+1)}}{1-\frac{20(3+\sqrt{3})-a}{20(\sqrt{3}+1)}•\frac{a}{20(\sqrt{3}+1)}}$=$\frac{400(4\sqrt{3}+6)}{[a-10(3+\sqrt{3})]^{2}+300(4+2\sqrt{3})}$,
∴a=40m,即P在A处,观察古塔DC的视角∠CPD最大.
点评 本题考查利用数学知识解决实际问题,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图,ABCD是正方形,SA⊥平面ABCD,BK⊥SC于点K,连接DK,求证:
如图,ABCD是正方形,SA⊥平面ABCD,BK⊥SC于点K,连接DK,求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在三棱柱ABC-A1B1C1中,E∈BC,F∈B1C1,EF∥C1C,点M∈侧面AA1B1B,设点M,E,F确定平面γ.试作出平面γ与三棱柱ABC-A1B1C1表面的交线,并说明理由.
如图所示,在三棱柱ABC-A1B1C1中,E∈BC,F∈B1C1,EF∥C1C,点M∈侧面AA1B1B,设点M,E,F确定平面γ.试作出平面γ与三棱柱ABC-A1B1C1表面的交线,并说明理由.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com