
【题目】已知椭圆M:: ![]() +
+ ![]() =1(a>0)的一个焦点为F(﹣1,0),左右顶点分别为A,B.经过点F的直线l与椭圆M交于C,D两点.
=1(a>0)的一个焦点为F(﹣1,0),左右顶点分别为A,B.经过点F的直线l与椭圆M交于C,D两点.
(1)求椭圆方程;
(2)当直线l的倾斜角为45°时,求线段CD的长;
(3)记△ABD与△ABC的面积分别为S1和S2 , 求|S1﹣S2|的最大值.
【答案】
(1)解:因为F(﹣1,0)为椭圆的焦点,所以c=1,又b2=3,
所以a2=4,所以椭圆方程为 ![]() =1;
=1;
(2)解:因为直线的倾斜角为45°,所以直线的斜率为1,
所以直线方程为y=x+1,和椭圆方程联立得到
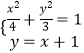 ,消掉y,得到7x2+8x﹣8=0,
,消掉y,得到7x2+8x﹣8=0,
所以△=288,x1+x2= ![]() ,x1x2=﹣
,x1x2=﹣ ![]() ,
,
所以|CD|= ![]() |x1﹣x2|=
|x1﹣x2|= ![]() ×
× ![]() =
= ![]() ;
;
(3)解:当直线l无斜率时,直线方程为x=﹣1,
此时D(﹣1, ![]() ),C(﹣1,﹣
),C(﹣1,﹣ ![]() ),△ABD,△ABC面积相等,|S1﹣S2|=0,
),△ABD,△ABC面积相等,|S1﹣S2|=0,
当直线l斜率存在(显然k≠0)时,设直线方程为y=k(x+1)(k≠0),
设C(x1,y1),D(x2,y2),
和椭圆方程联立得到 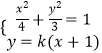 ,消掉y得(3+4k2)x2+8k2x+4k2﹣12=0,
,消掉y得(3+4k2)x2+8k2x+4k2﹣12=0,
显然△>0,方程有根,且x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
此时|S1﹣S2|=2||y1|﹣|y2||=2|y1+y2|=2|k(x2+1)+k(x1+1)|
=2|k(x2+x1)+2k|= ![]() =
= ![]() ≤
≤ ![]() =
= ![]() =
= ![]() ,(k=
,(k= ![]() 时等号成立)
时等号成立)
所以|S1﹣S2|的最大值为 ![]() .
.
【解析】(1)由焦点F坐标可求c值,根据a,b,c的平方关系可求得a值;(2)写出直线方程,与椭圆方程联立消掉y得关于x的一元二次方程,利用韦达定理及弦长公式即可求得|CD|;(3)当直线l不存在斜率时可得,|S1﹣S2|=0;当直线l斜率存在(显然k≠0)时,设直线方程为y=k(x+1)(k≠0),与椭圆方程联立消y可得x的方程,根据韦达定理可用k表示x1+x2 , x1x2 , |S1﹣S2|可转化为关于x1 , x2的式子,进而变为关于k的表达式,再用基本不等式即可求得其最大值;
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识,掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
【题目】已知y=f(x+1)是定义在R上的周期为2的偶函数,当x∈[1,2)时,f(x)=log2x,设a=f( ![]() ),
), ![]() ,c=f(1),则a,b,c的大小关系为( )
,c=f(1),则a,b,c的大小关系为( )
A.a<c<b
B.c<a<b
C.b<c<a
D.c<b<a
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数y=f(x)的定义域为R,并且满足f(x+y)=f(x)+f(y), ![]() ,且当x>0时,f(x)>0.
,且当x>0时,f(x)>0.
(1)求f(0)的值;
(2)判断函数的奇偶性;
(3)如果f(x)+f(2+x)<2,求x取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学名著《九章算术》中有这样一个问题:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟.羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比例偿还,他们各应偿还多少?已知牛、马、羊的主人各应偿还![]() 升,
升, ![]() 升,
升, ![]() 升,1斗为10升,则下列判断正确的是( )
升,1斗为10升,则下列判断正确的是( )
A. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
B. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
C. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
D. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正四棱锥![]() 中,已知异面直线
中,已知异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ,给出下面三个命题:
,给出下面三个命题:
![]() :若
:若![]() ,则此四棱锥的侧面积为
,则此四棱锥的侧面积为![]() ;
;
![]() :若
:若![]() 分别为
分别为![]() 的中点,则
的中点,则![]() 平面
平面![]() ;
;
![]() :若
:若![]() 都在球
都在球![]() 的表面上,则球
的表面上,则球![]() 的表面积是四边形
的表面积是四边形![]() 面积的
面积的![]() 倍.
倍.
在下列命题中,为真命题的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知随机变量X服从正态分布N(μ,σ2),且P(μ﹣2σ<X<μ+2σ)=0.954 4,P(μ﹣σ<X<μ+σ)=0.6826.若μ=4,σ=1,则P(5<X<6)=( )
A.0.1359
B.0.1358
C.0.2718
D.0.2716
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对甲、乙两名篮球运动员分别在100场比赛中的得分情况进行统计,做出甲的得分频率分布直方图如图所示,列出乙的得分统计表如表所示:
分值 | [0,10) | [10,20) | [20,30) | [30,40) |
场数 | 10 | 20 | 40 | 30 |
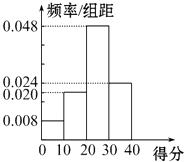
(1)估计甲在一场比赛中得分大于等于20分的概率.
(2)判断甲、乙两名运动员哪个成绩更稳定.(结论不要求证明)
(3)试利用甲的频率分布直方图估计甲每场比赛的平均得分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com