
| A. | “若a>1,则a2>1”的否命题是“若a>1,则a2≤1” | |
| B. | {an}为等比数列,则“a1<a2<a3”是“a4<a5”的既不充分也不必要条件 | |
| C. | 若a,b∈R,则|a|+|b|>1是|a+b|>1的充分而不必要条件 | |
| D. | “$tanα≠\sqrt{3}$”必要不充分条件是“$α≠\frac{π}{3}$” |
分析 由命题的否命题,既对条件否定,也对结论否定,即可判断A;
运用等比数列的通项公式,可得首项与公比的关系,判断单调性,结合充分必要条件定义,即可判断B;
由绝对值不等式的性质:|a|+|b|≥|a+b|,结合充分必要条件的定义,即可判断C;
由等价命题“tanα=$\sqrt{3}$”是“α=$\frac{π}{3}$”的必要不充分条件,结合充分必要条件的定义,即可判断D.
解答 解:对A,“若a>1,则a2>1”的否命题是“若a≤1,则a2≤1”,故A错;
对B,{an}为公比为q的等比数列,则“a1<a2<a3”即为a1<a1q<a1q2,
可得a1>0,q>1或a1<0,0<q<1,{an}为递增数列,可得“a4<a5”;
若“a4<a5”,即为a1q3<a1q4,可得a1>0,q>1或q<0,推不出“a1<a2<a3”.
则“a1<a2<a3”是“a4<a5”的充分不必要条件,故B错;
对C,若a,b∈R,由|a|+|b|≥|a+b|,可得|a|+|b|>1是|a+b|>1的必要而不充分条件,故C错;
对D,“$tanα≠\sqrt{3}$”必要不充分条件是“$α≠\frac{π}{3}$”
?“tanα=$\sqrt{3}$”是“α=$\frac{π}{3}$”的必要不充分条件,故D正确.
故选:D.
点评 本题考查四种命题和充分必要条件的判断,考查等比数列的单调性和绝对值不等式的性质,考查判断能力,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
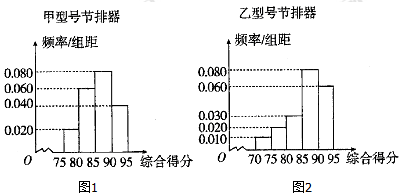
| 综合得分k的范围 | 节排器等级 | 节排器利润率 |
| k≥85 | 一级品 | a |
| 75≤k<85 | 二级品 | 5a2 |
| 70≤k<75 | 三级品 | a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0] | B. | (-1,0) | C. | [0,1] | D. | (0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{4}$ | B. | -$\frac{\sqrt{2}}{4}$ | C. | $\frac{3}{4}$ | D. | -$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 对于线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,直线必经过点 $({\overline x,\overline y})$; | |
| B. | 茎叶图的优点在于它可以保存原始数据,并且可以随时记录; | |
| C. | 用秦九韶算法求多项式f(x)=3x5-2x3+6x2+x+1=2时的值时,v2=14; | |
| D. | 将一组数据中的每一个数据都加上或减去同一个常数后,方差恒不变. |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有极大值,没有极小值 | B. | 没有极大值,有极小值 | ||
| C. | 既有极大值,也有极小值 | D. | 既无极大值,也没有极小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com