
(2007
江苏淮阴)已知动圆过定点P(1,0),且与定直线l:x=-1相切,点C在l上.(1)
求动圆圆心的轨迹M的方程.(2)
设过点P,且斜率为 的直线与曲线M相交于A、B两点.
的直线与曲线M相交于A、B两点.
①问:△
ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由.②当△
ABC为钝角三角形时,求这时点C的纵坐标的取值范围.|
如下图, (1)设M(x,y),依题意有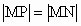 , ,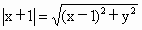 .化简得: .化简得: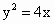 . .
(2) ①依题意得,直线AB的方程为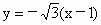 .由 .由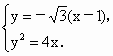 消y得 消y得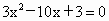 ,解得 ,解得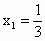 , ,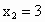 .所以A点坐标为 .所以A点坐标为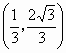 ,B点坐标为 ,B点坐标为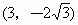 , ,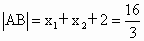 . .
假设存在点 C(-1,y),使△ABC为正三角形,则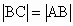 且 且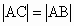 ,即 ,即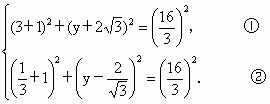
由①-②得 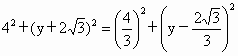 ,解得 ,解得 . .
但 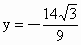 不符合①, 不符合①,
所以由①,②组成的方程组无解. 因此,直线 l上不存在点C,使得△ABC是正三角形.
②解法一:设 C(-1,y)使△ABC成纯角三角形,由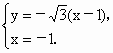 得 得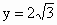 , ,
即当点 C的坐标为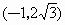 时,A、B、C三点共线,故 时,A、B、C三点共线,故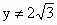 . .
又 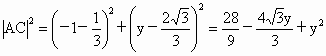 , ,
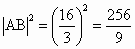 . .
当∠ CAB为钝角时,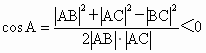 . .
即 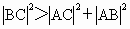 , ,
即 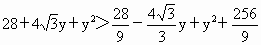 ,即 ,即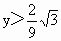 时,∠CAB为钝角. 时,∠CAB为钝角.
当 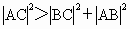 ,即 ,即
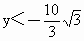 时,∠CBA为钝角. 时,∠CBA为钝角.
又 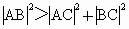 ,即 ,即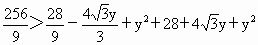 , ,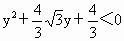 , ,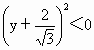 . .
该不等式无解,所以∠ ACB不可能为钝角.因此,当△ ABC为钝角三角形时,点C的纵坐标y的取值范围是
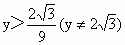 . .
解法二:以 AB为直径的圆的方程为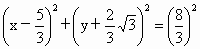 . .
圆心 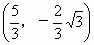 到直线l:x=-1的距离为 到直线l:x=-1的距离为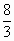 ,所以,以AB为直径的圆与直线l相切于点 ,所以,以AB为直径的圆与直线l相切于点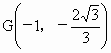  . .
当直线 l上的C点与G重合时,∠ACB为直角,当C与G点不重合,且A、B、C三点不共线时,∠ACB为锐角,即△ABC中,∠ACB不可能是钝角.因此,要使△ ABC为钝角三角形,只可能是∠CAB或∠CBA为钝角.过点 A且与AB垂直的直线方程为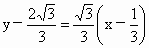 . .
令 x=-1得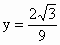 . .
过点 B且与AB垂直的直线方程为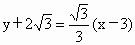 . .
令 x=-1得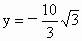 . .
又由 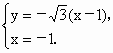 解得 解得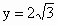 , ,
所以,当点 C的坐标为(-1,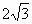 )时,A、B、C三点共线,不构成三角形. )时,A、B、C三点共线,不构成三角形.
因此,当△ ABC为钝角三角形时,点C的纵坐标y的取值范围是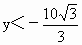 或 或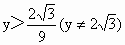 . . |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com