Question

已知sinθ+cosθ=，θ∈(0，π)，求tanθ的值.

Answer 1

解析一：由sinθ+cosθ=,                           ①

得1+2sinθcosθ=，即2sinθcosθ=-.

又0＜θ＜π，

∴cosθ＜0,

1-2sinθcosθ=，

即(cosθ-sinθ)²=.

∴sinθ-cosθ=.                                      ②

联立①②解方程组得

因此tanθ==-.

解析二：由sinθ+cosθ=,得

=,

即=.

∴3tan²-5tan²-2=0.

解得tan=2或tan=-.

∵0＜θ＜π,

∴0＜＜,tan＞0.

∴tan=2.

∴tanθ===-.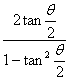

解析三：由sinθ+cosθ=,即sin(θ+)=＜,

∴＜θ+＜π,＜θ＜.

∴tanθ＜-1,=,=.

整理得12tan²θ+25tanθ+12=0.

解得tanθ=-或tanθ=-(舍去).

〔或由sin(θ+)=及＜θ+＜π,得

cos(θ+)=-,

∴tan(θ+)==-,

即=-,解得tanθ=-〕

解析四：由sinθ+cosθ=，

即sin(θ+)=＜,∴＜θ+＜π.

∴θ+=π-arcsin,

即θ=-arcsin.tanθ===-.

点评：解析一主要体现了平方关系的使用，用sinθ+cosθ表示sinθcosθ，进而表示sinθ-cosθ；解析二是利用二倍角公式齐次化切构造tan的方程求解；解析三是利用平方关系构造了关于tanθ的方程求解；解析四是根据已知条件先求角，然后再求值.本题通过一题多解，可以总结利用三角公式求值的解题技巧，提高三角恒等变形的能力.