Question

12．已知函数f（x）=e^x，g（x）=x²+（1-t）x+1（t＜0），h（x）=k（x+1）（k＞0）（e为自然对数的底数）．
（1）当函数f（x）的图象恒在h（x）的图象上方时，求实数k的取值范围；
（2）若存在x₁，x₂∈[0，1]，使得f（x₁）g（x₁）＞2f（x₂）g（x₁）成立，求实数t的取值范围．

Answer 1

分析 （1）作出函数的图象，利用导数的几何意义求出切线斜率，利用数形结合即可得到结论；
（2）由题意可得$\frac{g（{x}_{2}）}{f（{x}_{2}）}＞2•\frac{g（{x}_{1}）}{f（{x}_{1}）}$成立，令m（x）=$\frac{g（x）}{f（x）}$，则有在[0，1]有m（x）的最大值大于最小值的2倍，求出m（x）的导数，对t讨论，由单调性求得最值，解不等式即可得到所求范围．

解答 解：（1）若函数f（x）图象恒在函数h（x）图象的上方（没有交点），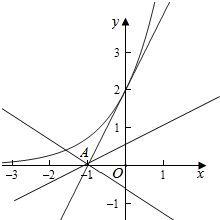
则e^x＞k（x+1），
当k＞0时，g（x）=k（x+1）过定点（-1，0），
函数f（x）的导数为f′（x）=e^x，
设h（x）=k（x+1）与f（x）=e^x的切点为（a，b），则对应的切线斜率k=f′（a）=e^a，
则对应的切线方程为y-e^a=e^a（x-a），
∵直线过点（-1，0），
∴-e^a=e^a（-1-a），
解得a=0，此时切线斜率k=f′（0）=1，
即此时k=1，
则解得0＜k＜1；
（2）存在x₁，x₂∈[0，1]，使得f（x₁）g（x₂）＞2f（x₂）g（x₁）成立，
即有$\frac{g（{x}_{2}）}{f（{x}_{2}）}＞2•\frac{g（{x}_{1}）}{f（{x}_{1}）}$成立，
令m（x）=$\frac{g（x）}{f（x）}$，即在[0，1]有m（x）的最大值大于最小值的2倍，
由m′（x）=$\frac{-（x-1）（x-t）}{{e}^{x}}$，
当t≤0时，区间[0，1]为增区间，m（0）为最小值，等于$\frac{1}{{e}^{0}}=1$；
m（1）为最大值，等于$\frac{3-t}{e}$．
由$\frac{3-t}{e}＞2$，得t＜3-2e；
当0＜t＜1时，区间（0，t）递减，区间（t，1）递增，
m（t）取得最小值，等于$\frac{1+t}{{e}^{t}}$；
m（0）或m（1）取得最大值，即为1或$\frac{3-t}{e}$．
即有1＞2•$\frac{1+t}{{e}^{t}}$或$\frac{3-t}{e}$＞2•$\frac{1+t}{{e}^{t}}$，
∵$（\frac{{e}^{t}}{1+t}）′=\frac{t•{e}^{t}}{（1+t）^{2}}＞0$在（0，1）上成立，
则1＜$\frac{{e}^{t}}{1+t}$＜$\frac{e}{2}$，
∴1＞2•$\frac{1+t}{{e}^{t}}$无解；
又$（{e}^{t}-2e•\frac{1+t}{3-t}）′={e}^{t}-2e•\frac{4}{（t-3）^{2}}＜0$在（0，1）上成立，
即有e^t-2e•$\frac{1+t}{3-t}＜1-\frac{2e}{3}＜0$，
则$\frac{3-t}{e}$＞2•$\frac{1+t}{{e}^{t}}$无解；
当t≥1时，区间[0，1]为减区间，m（0）为最大值，等于$\frac{1}{{e}^{0}}=1$；
m（1）为最小值，等于$\frac{3-t}{e}$．
由2•$\frac{3-t}{e}$＜1，即有t＞3-$\frac{e}{2}$．
综上可得，t的范围是t＜3-2e或t＞3-$\frac{e}{2}$．

点评 本题考查函数恒成立问题，主要考查了导数的运用，训练了存在性问题的解法，正确运用分类讨论的思想方法和函数的单调性是解题的关键，是难题．