练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图，直线AB、BC、CA两两相交，交点分别为A、B、C，判断这三条直线是否共面并说明理由.回答是肯定的.这三条直线共面，理由如下：∵直线AB和AC相交于点A ，∴直线AB和AC_________（推论2）.?

    ∵B_______直线AB，C_________直线AC ，∴B________α,C___________α.∴BC______α(公理______）.因此，直线AB、BC、CA都在平面_________内，即它们_________.

    确定一个平面α　∈　∈　∈　∈　?　1　α　共面

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

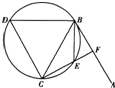    （选修4-1：几何证明选讲）
    如图，直线AB为圆的切线，切点为B，点C在圆上，∠ABC的角平分线BE交圆于点E，DB垂直BE交圆于D．
    （Ⅰ）证明：DB=DC；
    （Ⅱ）设圆的半径为1，BC=
    		3
    ，延长CE交AB于点F，求△BCF外接圆的半径．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，直线AB与椭圆：
    x2
    a2
    +
    y2
    b2
    =1    （a＞b＞0）交于A，B两点，与x轴和y轴分别交于点P和点Q，点C是点A关于x轴的对称点，直线BC与x轴交于点R．
    （1）若点P为（6，0），点Q为（0，3），点A，B恰好是线段QP的两个三等分点．
    ①求椭圆的方程；
    ②过坐标原点O引△ABC外接圆的切线，求切线长；
    （2）当椭圆给定时，试探究OP•OR是否为定值？若是，请求出此定值；若不是，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    几何证明选讲   如图，直线AB为圆的切线，切点为B，点C在圆上，∠ABC的角平分线BE交圆于点E，DB垂直BE交圆于D。

    （Ⅰ）证明：DB=DC；

       （Ⅱ）设圆的半径为1，BC=  ，延长CE交AB于点F，求△BCF外接圆的半径。

    查看答案和解析>>

    科目：高中数学 来源：2013年全国普通高等学校招生统一考试理科数学（新课标1卷解析版） 题型：解答题

    （本小题满分10分）选修4—1：几何证明选讲   如图，直线AB为圆的切线，切点为B，点C在圆上，∠ABC的角平分线BE交圆于点E，DB垂直BE交圆于D。

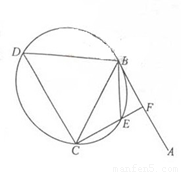
    （Ⅰ）证明：DB=DC；

    （Ⅱ）设圆的半径为1，BC=，延长CE交AB于点F，求△BCF外接圆的半径。

     

    查看答案和解析>>

    同步练习册答案