
【题目】设椭圆方程![]() +
+![]() =1(a>b>0),椭圆上一点到两焦点的距离和为4,过焦点且垂直于x轴的直线交椭圆于A,B两点,AB=2.
=1(a>b>0),椭圆上一点到两焦点的距离和为4,过焦点且垂直于x轴的直线交椭圆于A,B两点,AB=2.
(1)求椭圆方程;
(2)若M,N是椭圆C上的点,且直线OM与ON的斜率之积为﹣![]() ,是否存在动点P(x0,y0),若
,是否存在动点P(x0,y0),若![]() =
=![]() +2
+2![]() ,有x02+2y02为定值
,有x02+2y02为定值
【答案】(1)![]() (2)存在这样的点P(x0,y0)
(2)存在这样的点P(x0,y0)
【解析】
试题分析:(1)由已知得2a=4,![]() ,由此能求出椭圆方程;(2)存在这样的点P
,由此能求出椭圆方程;(2)存在这样的点P![]() .设M
.设M ![]() ,N
,N ![]() ,由
,由![]() ,结合已知条件能推导出存在这样的点P(x0,y0)
,结合已知条件能推导出存在这样的点P(x0,y0)
试题解析:(1)因为2a=4,所以,a=2,(2分)
∵过焦点且垂直于x轴的直线交椭圆于A,B两点,AB=2.
∴由椭圆的对称性知,椭圆过点(c,1),即![]() ,(4分)
,(4分)
c2=4﹣b2,解得b2=2,椭圆方程为![]() .(7分)
.(7分)
(2)存在这样的点P(x0,y0).设M(x1,y1),N(x2,y2),
则kOMkON=![]() =﹣
=﹣![]() ,化简为x1x2+2y1y2=0,(9分)
,化简为x1x2+2y1y2=0,(9分)
∵M,N是椭圆C上的点,∴![]() ,
,![]() ,
,
由![]() =
=![]() ,得
,得 ,(12分)
,(12分)
∵![]() =(x1+2x2)2+(y1+2y2)2
=(x1+2x2)2+(y1+2y2)2
=(![]() )+4(
)+4(![]() )+4(x1x2+2y1y2)=4+4×4+0=20,
)+4(x1x2+2y1y2)=4+4×4+0=20,
即存在这样的点P(x0,y0).


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 分别为椭圆
分别为椭圆![]() :
:![]()
![]() 的左、右两个焦点.
的左、右两个焦点.
(Ⅰ)若椭圆![]() 上的点
上的点![]() 到
到![]() 、
、![]() 两点的距离之和等于6,写出椭圆
两点的距离之和等于6,写出椭圆![]() 的方程和焦点坐标;
的方程和焦点坐标;
(Ⅱ)设点![]() 是(1)中所得椭圆上的动点,求线段
是(1)中所得椭圆上的动点,求线段![]() 的中点M的轨迹方程.
的中点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() ,圆
,圆![]() .
.
(1)若过点![]() 的直线
的直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)圆![]() 是以1为半径,圆心在圆
是以1为半径,圆心在圆![]() :
:![]() 上移动的动圆 ,若圆
上移动的动圆 ,若圆![]() 上任意一点
上任意一点![]() 分别作圆
分别作圆![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若动圆![]() 同时平分圆
同时平分圆![]() 的周长、圆
的周长、圆![]() 的周长,则动圆
的周长,则动圆![]() 是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把离心率![]() 的双曲线
的双曲线![]() 称为黄金双曲线.给出以下几个说法:
称为黄金双曲线.给出以下几个说法:
①双曲线![]() 是黄金双曲线;
是黄金双曲线;
②若双曲线上一点![]() 到两条渐近线的距离积等于
到两条渐近线的距离积等于![]() ,则该双曲线是黄金双曲线;
,则该双曲线是黄金双曲线;
③若![]() 为左右焦点,
为左右焦点,![]() 为左右顶点,
为左右顶点,![]() 且
且![]() ,则该双曲线是黄金双曲线;
,则该双曲线是黄金双曲线;
④.若直线![]() 经过右焦点
经过右焦点![]() 交双曲线于
交双曲线于![]() 两点,且
两点,且![]() ,
,![]() ,则该双曲线是黄金双曲线;
,则该双曲线是黄金双曲线;
其中正确命题的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前三项分别为λ,6,3λ,前n项和为Sn,且Sk=165.
的前三项分别为λ,6,3λ,前n项和为Sn,且Sk=165.
(1)求λ及k的值;
(2)设bn=![]() ,且数列
,且数列![]() 的前n项和Tn,证明:
的前n项和Tn,证明:![]() ≤Tn<1.
≤Tn<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2016年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布如图所示.
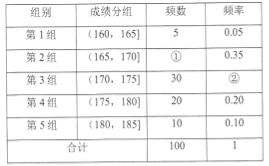
(1)请先求出频率分布表中①、②位置相应的数据,再画出频率分布直方图;
(2)该高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受考官的面试,求第4组至少有一名学生被考官面试的概率?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com