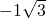已知函数f(x)=loga(1-x)+loga(x+3)(0<a<1)
(1)求函数f(x)的定义域;
(2)求函数f(x)的零点;
(3)若函数f(x)的最小值为-4,求a的值.
解:(1)要使函数有意义:则有
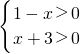
,解之得:-3<x<1,
则函数的定义域为:(-3,1)
(2)函数可化为f(x)=log
a(1-x)(x+3)=log
a(-x
2-2x+3)
由f(x)=0,得-x
2-2x+3=1,
即x
2+2x-2=0,
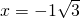
∵
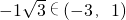
,∴函数f(x)的零点是
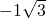
(3)函数可化为:
f(x)=log
a(1-x)(x+3)=log
a(-x
2-2x+3)=log
a[-(x+1)
2+4]
∵-3<x<1,∴0<-(x+1)
2+4≤4,
∵0<a<1,∴log
a[-(x+1)
2+4]≥log
a4,
即f(x)
min=log
a4,由log
a4=-4,得a
-4=4,
∴

分析:(1)根据对数的真数大于零,列出不等式组并求出解集,函数的定义域用集合或区间表示出来;
(2)利用对数的运算性质对解析式进行化简,再由f(x)=0,即-x
2-2x+3=1,求此方程的根并验证是否在函数的定义域内;
(3)把函数解析式化简后,利用配方求真数在定义域内的范围,再根据对数函数在定义域内递减,求出函数的最小值log
a4,得log
a4=-4利用对数的定义求出a的值.
点评:本题是关于对数函数的综合题,考查了对数的真数大于零、函数零点的定义和对数型的复合函数求最值,注意应在函数的定义域内求解.

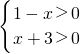 ,解之得:-3<x<1,
,解之得:-3<x<1,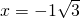
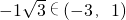 ,∴函数f(x)的零点是
,∴函数f(x)的零点是