
| | 非积极分子 | 积极分子 | 合计 |
| 男 | | 15 | 45 |
| 女 | | | |
| 合计 | | | |
| | 非积极分子 | 积极分子 | 合计 |
| 男 | 30 | 15 | 45 |
| 女 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
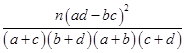 =
= =
=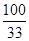 ≈3.030,可得没有理由认为“积极分子”与性别有关.
≈3.030,可得没有理由认为“积极分子”与性别有关.| | 非积极分子 | 积极分子 | 合计 |
| 男 | 30 | 15 | 45 |
| 女 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
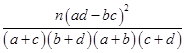 =
= =
=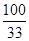 ≈3.030. 11分
≈3.030. 11分

科目:高中数学 来源:不详 题型:解答题
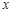 (万元)与销售额
(万元)与销售额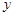 (万元)之间有如下的对应数据:
(万元)之间有如下的对应数据: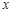 | 2 | 4 | 5 | 6 | 8 |
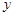 | 30 | 40 | 60 | 50 | 70 |
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
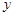 的值.
的值.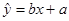 ,其中
,其中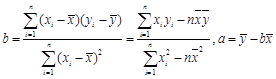 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
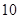 天空气质量指数(
天空气质量指数(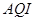 )和“
)和“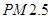 ”(直径小于等于
”(直径小于等于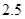 微米的颗粒物)
微米的颗粒物)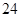 小时平均浓度的数据,空气质量指数(
小时平均浓度的数据,空气质量指数(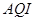 )小于
)小于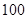 表示空气质量优良.
表示空气质量优良.| 日期编号 | 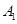 | 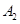 | 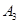 | 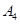 | 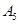 | 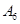 | 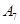 | 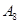 | 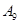 | 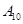 |
空气质量指数(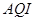 ) ) | 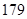 | 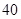 | 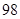 | 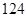 | 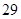 | 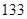 | 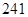 | 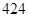 | 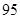 | 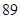 |
“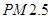 ” ”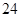 小时平均浓度( 小时平均浓度(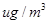 ) ) | 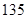 | 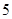 |  | 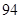 |  | 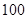 | 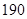 | 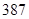 | 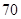 | 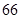 |
 为“抽取的两个日期中,当天‘
为“抽取的两个日期中,当天‘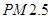 ’的
’的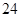 小时平均浓度不超过
小时平均浓度不超过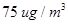 ”,求事件
”,求事件 发生的概率;
发生的概率;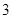 天,记
天,记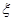 为“
为“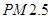 ”
”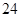 小时平均浓度不超过
小时平均浓度不超过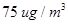 的天数,求
的天数,求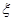 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
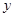 (单位:
(单位: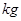 )与身高
)与身高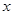 (单位:
(单位: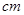 )具有线性相关关系,根据一组样本数据
)具有线性相关关系,根据一组样本数据 ,用最小二乘法建立的回归方程为
,用最小二乘法建立的回归方程为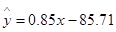 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )A.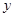 与 与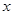 具有正的线性相关关系 具有正的线性相关关系 |
B.回归直线过样本点的中心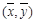 |
| C.若该大学某女生身高增加lcm,则其体重约增加0.85kg |
| D.若该大学某女生身高为170cm,则可断定其体重必为58.79kg |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
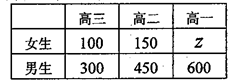
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
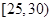 ,第2组
,第2组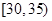 ,第3组
,第3组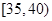 ,第4组
,第4组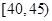 ,第5组
,第5组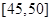 ,由统计的数据得到的频率分布直方图如图所示,在其右面的表是年龄的频率分布表。
,由统计的数据得到的频率分布直方图如图所示,在其右面的表是年龄的频率分布表。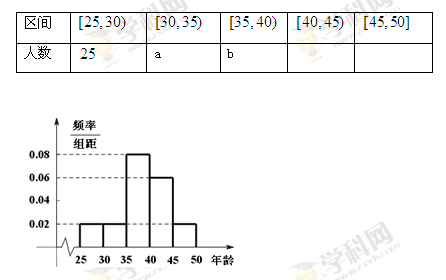
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
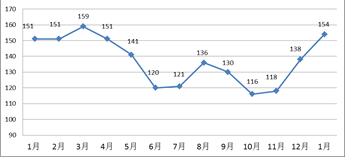
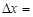 本月价格指数
本月价格指数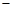 上月价格指数.规定:当
上月价格指数.规定:当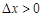 时,称本月价格指数环比增长;
时,称本月价格指数环比增长;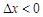 时,称本月价格指数环比下降;当
时,称本月价格指数环比下降;当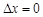 时,称本月价格指数环比持平.
时,称本月价格指数环比持平.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 零件数x/个 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| 加工时间y/分 | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com