
【题目】某车间有50名工人,要完成150件产品的生产任务,每件产品由3个![]() 型零件和1个
型零件和1个![]() 型零件配套组成,每个工人每小时能加工5个
型零件配套组成,每个工人每小时能加工5个![]() 型零件或者3个
型零件或者3个![]() 型零件,现在把这些工人分成两组同时工作(分组后人数不再进行调整),每组加工同一种型号的零件.设加工
型零件,现在把这些工人分成两组同时工作(分组后人数不再进行调整),每组加工同一种型号的零件.设加工![]() 型零件的工人数为
型零件的工人数为![]() 名
名![]() .
.
(1)设完成![]() 、
、![]() 型零件加工所需的时间分别为
型零件加工所需的时间分别为![]() 、
、![]() 小时,写出
小时,写出![]() 与
与![]() 的解析式;
的解析式;
(2)当![]() 取何值时,完成全部生产任务的时间最短?
取何值时,完成全部生产任务的时间最短?
【答案】(1)![]() (
(![]() ,且
,且![]() );
);![]() (
(![]() ,且
,且![]() );(2)为了在最短时间内完成生产任务,
);(2)为了在最短时间内完成生产任务,![]() 应取32.
应取32.
【解析】
(1)分别计算得到![]() 和
和![]() ,再计算定义域得到答案.
,再计算定义域得到答案.
(2)根据![]() 和
和![]() 的大小关系得到
的大小关系得到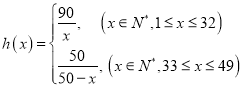 ,分别计算函数的最小值得到答案.
,分别计算函数的最小值得到答案.
(1)生产150件产品,需加工![]() 型零件450个,
型零件450个,
则完成![]() 型零件加工所需时间
型零件加工所需时间![]() (
(![]() ,且
,且![]() ).
).
生产150件产品,需加工![]() 型零件150个,
型零件150个,
则完成![]() 型零件加工所需时间
型零件加工所需时间![]() (
(![]() ,且
,且![]() ).
).
(2)设完成全部生产任务所需时间为![]() 小时,则
小时,则![]() 为
为![]() 与
与![]() 的较大者.
的较大者.
令![]() ,即
,即![]() ,解得
,解得![]() .
.
所以,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
故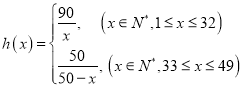 .
.
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上单调递减,
上单调递减,
则![]() 在
在![]() 上的最小值为
上的最小值为![]() (小时);
(小时);
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上单调递增,
上单调递增,
则![]() 在
在![]() 上的最小值为
上的最小值为![]() (小时);
(小时);
∵![]() ,∴
,∴![]() 在
在![]() 上的最小值为
上的最小值为![]()
∴![]() .
.
为了在最短时间内完成生产任务,![]() 应取32.
应取32.


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() ,下述四个结论:
,下述四个结论:
①![]() 是偶函数;
是偶函数;
②![]() 的最小正周期为
的最小正周期为![]() ;
;
③![]() 的最小值为0;
的最小值为0;
④![]() 在
在![]() 上有3个零点
上有3个零点
其中所有正确结论的编号是( )
A.①②B.①②③C.①③④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程
的参数方程![]() (
(![]() 为参数).以
为参数).以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)直线![]() 的极坐标方程是
的极坐标方程是![]() ,射线
,射线![]() 与圆
与圆![]() 的交点为
的交点为![]() ,
,![]() ,与直线
,与直线![]() 的交点为
的交点为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:![]() =2px经过点
=2px经过点![]() (1,2).过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.
(1,2).过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.
(Ⅰ)求直线l的斜率的取值范围;
(Ⅱ)设O为原点,![]() ,
,![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第![]() 届冬奥会将于
届冬奥会将于![]() 年在中国北京和张家口举行,为宣传冬奥会,让更多的人了解、喜爱冰雪项目,某大学举办了冬奥会知识竞赛,并从中随机抽取了
年在中国北京和张家口举行,为宣传冬奥会,让更多的人了解、喜爱冰雪项目,某大学举办了冬奥会知识竞赛,并从中随机抽取了![]() 名学生的成绩,绘制成如图所示的频率分布直方图.
名学生的成绩,绘制成如图所示的频率分布直方图.
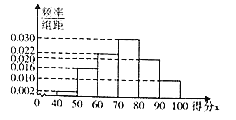
(Ⅰ)试根据频率分布直方图估计这![]() 名学生的平均成绩(同一组数据用该组区间的中点值代替);
名学生的平均成绩(同一组数据用该组区间的中点值代替);
(Ⅱ)若采用分层抽样的方法从![]() 、
、![]() 这两个分数段中抽取
这两个分数段中抽取![]() 人,求从这两个分数段中应分别抽取多少人?
人,求从这两个分数段中应分别抽取多少人?
(Ⅲ)从(Ⅱ)中抽取的![]() 人中随机抽取
人中随机抽取![]() 人到某社区开展冬奥会宜传活动,求抽取的
人到某社区开展冬奥会宜传活动,求抽取的![]() 人成绩均在
人成绩均在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的方程为
的方程为![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 有且仅有三个公共点,求
有且仅有三个公共点,求![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com