
【题目】用长为18 m的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
【答案】解:设长方体的宽为x(m),则长为2x(m),高为
![]() .
.
故长方体的体积为
![]()
从而 ![]()
令V′(x)=0,解得x=0(舍去)或x=1,因此x=1.
当0<x<1时,V′(x)>0;当1<x< ![]() 时,V′(x)<0,
时,V′(x)<0,
故在x=1处V(x)取得极大值,并且这个极大值就是V(x)的最大值。
从而最大体积V=V′(x)=9×12-6×13(m3),此时长方体的长为2 m,高为1.5 m.
答:当长方体的长为2 m时,宽为1 m,高为1.5 m时,体积最大,最大体积为3 m3。
【解析】设长方体的宽为xm,根据题意将长和宽用x表示出来,然后根据长方体体积公式用x表示出体积V,利用导数V![]() (x)讨论V(x)在定义域内的单调性,从而求出V(x)在定义域内的最大值及取得最大值时x的值.
(x)讨论V(x)在定义域内的单调性,从而求出V(x)在定义域内的最大值及取得最大值时x的值.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,已知双曲线 ![]() =1(a>0,b>0)的左右焦点分别为F1 , F2 , |F1F2|=4,P是双曲线右支上的一点,F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=1,则双曲线的离心率是( )
=1(a>0,b>0)的左右焦点分别为F1 , F2 , |F1F2|=4,P是双曲线右支上的一点,F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=1,则双曲线的离心率是( ) 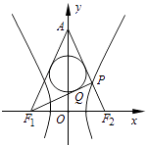
A.3
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知锐角△ABC中,角A、B、C所对的边分别为a、b、c,若a=2,b2+c2﹣bc=4,则△ABC的面积的取值范围是( )
A.( ![]() ,
, ![]() ]
]
B.(0, ![]() ]
]
C.( ![]() ,
, ![]() ]
]
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB、CD是圆的两条平行弦,BE∥AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.
(1)求AC的长;
(2)试比较BE与EF的长度关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AE:EB=1:2. 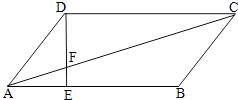
(1)求△AEF与△CDF的周长比;
(2)如果△AEF的面积等于6cm2 , 求△CDF的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,且
,且![]() .
.
(1)当![]() 时,写出
时,写出![]() 的通项公式(直接写出答案,无需过程);
的通项公式(直接写出答案,无需过程);
(2)求最小整数![]() ,使得当
,使得当![]() 时,
时, ![]() 是单调递增数列;
是单调递增数列;
(3)是否存在![]() 使得
使得![]() 是等比数列?若存在请求出;若不存在请说明理由.
是等比数列?若存在请求出;若不存在请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2015﹣2016赛季CBA联赛中,某队甲、乙两名球员在前10场比赛中投篮命中情况统计如下表(注:表中分数 ![]() ,N表示投篮次数,n表示命中次数),假设各场比赛相互独立.
,N表示投篮次数,n表示命中次数),假设各场比赛相互独立.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲 |
|
|
|
|
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
|
|
|
|
根据统计表的信息:
(1)从上述比赛中等可能随机选择一场,求甲球员在该场比赛中投篮命中率大于0.5的概率;
(2)试估计甲、乙两名运动员在下一场比赛中恰有一人命中率超过0.5的概率;
(3)在接下来的3场比赛中,用X表示这3场比赛中乙球员命中率超过0.5的场次,试写出X的分布列,并求X的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com