
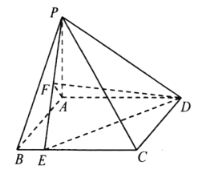
【题目】四棱锥P﹣ABCD中,AD![]() BC,BC⊥CD,BC=CD=2AD=2,PD=
BC,BC⊥CD,BC=CD=2AD=2,PD=![]() ,侧面PBC是等边三角形.
,侧面PBC是等边三角形.
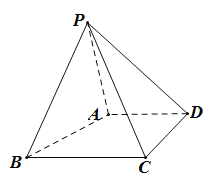
(1)证明:PA⊥平面PBC;
(2)求BC与平面PCD所成角的余弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)先证明BC⊥平面PAM,得到BC⊥PA,又PA⊥PM,根据线面垂直的判定定理证明即可;
(2)BC=2,过B作BH⊥平面PCD,连接CH,则∠BCH为BC与平面PCD所成的角,利用等体积转化法求出BH,再利用三角公式求出即可.
(1)取BC的中点M连接AM,PM,所以PM⊥BC,AM⊥BC,
PM∩AM=M,所以BC⊥平面PAM,所以BC⊥PA,所以PA⊥AD,PA=1,
所以PA2+PM2=1+3=4=AM2,得PA⊥PM,又PA⊥BC,PM∩BC=M,
故PA⊥平面PBC;
(2)BC=2,过B作BH⊥平面PCD,连接CH,则∠BCH为BC与平面PCD所成的角,
设P到底面ABCD的距离为h,h=![]() ,
,
由PC=CD=2,PD=![]() ,所以
,所以![]() =
=![]() ,
,
由等体积法,Vp﹣BCD=VB﹣PDC,所以![]() ,得BH=
,得BH=![]() ,
,
所以sin∠BCH=![]() ,所以cos∠BCH=
,所以cos∠BCH=![]() .
.



 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
:![]() (
(![]() ,
,![]() )的右焦点
)的右焦点![]() ,且椭圆
,且椭圆![]() 过点
过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设动直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() ,
,![]() ,且
,且![]() 的面积
的面积![]() .
.
①求证:![]() 为定值;
为定值;
②设直线![]() 的中点
的中点![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 截直线
截直线![]() 所得线段的中点坐标为
所得线段的中点坐标为![]() ,求
,求![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,合肥一中积极开展美丽校园建设,现拟在边长为0.6千米的正方形地块![]() 上划出一片三角形地块
上划出一片三角形地块![]() 建设小型生态园,点
建设小型生态园,点![]() 分别在边
分别在边![]() 上.
上.
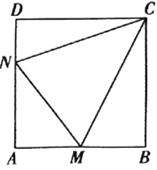
(1)当点![]() 分别时边
分别时边![]() 中点和
中点和![]() 靠近
靠近![]() 的三等分点时,求
的三等分点时,求![]() 的余弦值;
的余弦值;
(2)实地勘察后发现,由于地形等原因,![]() 的周长必须为1.2千米,请研究
的周长必须为1.2千米,请研究![]() 是否为定值,若是,求此定值,若不是,请说明理由.
是否为定值,若是,求此定值,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设F1,F2是椭圆C:![]() (a>b>0)的左、右焦点,直线y=kx(k>0)与椭圆C交于A,B.已知椭圆C的焦距是2,四边形AF1BF2的周长是4
(a>b>0)的左、右焦点,直线y=kx(k>0)与椭圆C交于A,B.已知椭圆C的焦距是2,四边形AF1BF2的周长是4![]() .
.
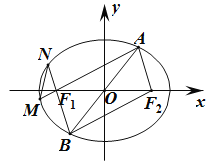
(1)求椭圆C的方程;
(2)直线AF1,BF1分别与椭圆C交于M,N,求△MNF1面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面四边形ABCD中,E、F是AD、BD中点,AB=AD=CD=2, BD=2![]() ,∠BDC=90°,将△ABD沿对角线BD折起至△
,∠BDC=90°,将△ABD沿对角线BD折起至△![]() ,使平面
,使平面![]() ⊥平面BCD,则四面体
⊥平面BCD,则四面体![]() 中,下列结论不正确是 ( )
中,下列结论不正确是 ( )
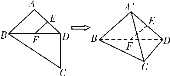
A. EF∥平面![]()
B. 异面直线CD与![]() 所成的角为90°
所成的角为90°
C. 异面直线EF与![]() 所成的角为60°
所成的角为60°
D. 直线![]() 与平面BCD所成的角为30°
与平面BCD所成的角为30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中,![]() 平面ABCD,四边形ABCD是矩形,且
平面ABCD,四边形ABCD是矩形,且![]() ,
,![]() ,E是棱BC上的动点,F是线段PE的中点.
,E是棱BC上的动点,F是线段PE的中点.
(Ⅰ)求证:![]() 平面ADF;
平面ADF;
(Ⅱ)若直线DE与平面ADF所成角为30°,求EC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且an=![]() (3n+Sn)对一切正整数n成立
(3n+Sn)对一切正整数n成立
(I)证明:数列{3+an}是等比数列,并求出数列{an}的通项公式;
(II)设![]() ,求数列
,求数列![]() 的前n项和Bn;
的前n项和Bn;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com