
【题目】如图,△ABC为一个等腰三角形形状的空地,腰CA的长为3(百米),底AB的长为4(百米).现决定在空地内筑一条笔直的小路EF(宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为S1和S2 . 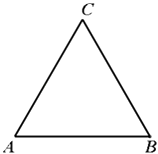
(1)若小路一端E为AC的中点,求此时小路的长度;
(2)求 ![]() 的最小值.
的最小值.
【答案】
(1)解:因为:AE=CE= ![]() AE+4>CE+3 所以F不在BC上,
AE+4>CE+3 所以F不在BC上,
AE+AF+EF=CE+CB+FB+EF
所以AE=CE AF=CB+BF 4﹣BF=BF+3 BF= ![]()
cosA= ![]() =
= ![]()
所以EF2=AE2+AF2﹣2AE×AF×cosA= ![]()
所以EF= ![]()
E为AC中点时,此时小路的长度为 ![]() 百米
百米
(2)解:若E、F分别在AC和AB上,
sinA= ![]()
设AE=x,AF=y,
所以S2= ![]() xysinA=
xysinA= ![]()
S1=S三角形ABC﹣S2=2 ![]() ﹣S2
﹣S2
因为x+y=3﹣x+4﹣y+3
所以x+y=5
![]() =
=  ﹣1
﹣1
xy≤ 
当且仅当x=y= ![]() 时取等号
时取等号
所以 ![]() =
= ![]()
当且仅当x=y= ![]() 时取等号
时取等号
最小值是 ![]()
若E、F分别在AC和BC上,
![]() sinC=
sinC= ![]()
设CE=x,CF=y
同上可得 ![]() ≥
≥ ![]()
当且仅当x=y= ![]() 取等号
取等号
若E、F分别在AC和BC上,最小值是 ![]()
【解析】(1)根据题意可知F不在BC上,根据余弦定理求出cosA的值,然后根据余弦定理求出EF的长即可;(2)若E、F分别在AC和AB上,设AE=x,AF=y,然后利用三角形的面积公式求出S2和S1=S三角形ABC﹣S2=,再根据基本不等式求出比值的最值即可,若E、F分别在AC和BC上,设CE=x,CF=y,同上根据基本不等式求出比值的最值即可.
【考点精析】本题主要考查了函数的最值及其几何意义的相关知识点,需要掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值才能正确解答此题.


 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】某工厂为了解用电量y与气温x℃之间的关系,随机统计了5天的用电量与当天气温,得到如下统计表:
曰期 | 8月1曰 | 8月7日 | 8月14日 | 8月18日 | 8月25日 |
平均气温(℃) | 33 | 30 | 32 | 30 | 25 |
用电量(万度) | 38 | 35 | 41 | 36 | 30 |
![]() xiyi=5446,
xiyi=5446, ![]() xi2=4538,
xi2=4538, ![]() =
= 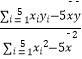 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
(1)请根据表中的数据,求出y关于x的线性回归方程.据气象預报9月3日的平均气温是 23℃,请预测9月3日的用电量;(结果保留整数)
(2)请从表中任选两天,记用电量(万度)超过35的天数为ξ,求ξ的概率分布列,并求其数学期望和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC, ![]() ,AB⊥AC,D是棱BB1的中点.
,AB⊥AC,D是棱BB1的中点. 
(Ⅰ)证明:平面A1DC⊥平面ADC;
(Ⅱ)求平面A1DC与平面ABC所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知x,y∈R,m+n=7,f(x)=|x﹣1|﹣|x+1|.
(1)解不等式f(x)≥(m+n)x;
(2)设max{a,b}= ![]() ,求F=max{|x2﹣4y+m|,|y2﹣2x+n|}的最小值.
,求F=max{|x2﹣4y+m|,|y2﹣2x+n|}的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一张边长为12cm的正方形纸片按如图(1)所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型,如图(2)所示放置.如果正四棱锥的主视图是等边三角形,如图(3)所示,则正四棱锥的体积是( ) 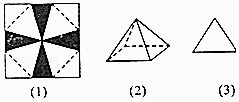
A.![]() cm3
cm3
B.![]() cm3
cm3
C.![]() cm3
cm3
D.![]() cm3
cm3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费用支出![]() 与销售额
与销售额![]() 之间有如下的对应数据(单位:万元):
之间有如下的对应数据(单位:万元):
![]()
(1)求![]() 关于
关于![]() 的线性回归直线方程;
的线性回归直线方程;
(2)据此估计广告费用为10万元时销售收入![]() 的值.
的值.
(附:对于线性回归方程![]() ,其中
,其中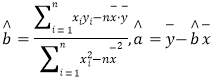 )
)
参考公式: 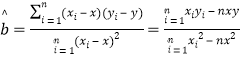
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市对贫困家庭自主创业给予小额贷款补贴,每户贷款为2万元,贷款期限有6个月、12个月、18个月、24个月、36个月五种,这五种贷款期限政府分别需要补助200元、300元、300元、400元,从2016年享受此项政策的困难户中抽取了100户进行了调查,选取贷款期限的频数如表:
贷款期限 | 6个月 | 12个月 | 18个月 | 24个月 | 36个月 |
频数 | 20 | 40 | 20 | 10 | 10 |
以上表各种贷款期限频率作为2017年贫困家庭选择各种贷款期限的概率.
(1)某小区2017年共有3户准备享受此项政策,计算其中恰有两户选择贷款期限为12个月的概率;
(2)设给享受此项政策的某困难户补贴为ξ元,写出ξ的分布列,若预计2017年全市有3.6万户享受此项政策,估计2017年该市共需要补贴多少万元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com