
【题目】如图,四棱锥P﹣ABCD中,所有棱长均为2,O是底面正方形ABCD中心,E为PC中点,则直线OE与直线PD所成角为( ) 
A.30°
B.60°
C.45°
D.90°
科目:高中数学 来源: 题型:
【题目】如图所示,某村积极开展“美丽乡村生态家园”建设,现拟在边长为1千米的正方形地块ABCD上划出一片三角形地块CMN建设美丽乡村生态公园,给村民休闲健身提供去处.点M,N分别在边AB,AD上. (Ⅰ)当点M,N分别是边AB,AD的中点时,求∠MCN的余弦值;
(Ⅱ)由于村建规划及保护生态环境的需要,要求△AMN的周长为2千米,请探究∠MCN是否为定值,若是,求出此定值,若不是,请说明理由.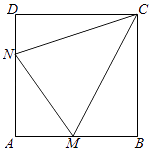
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣3)2+(y﹣4)2=4,直线l过定点A(1,0).
(1)若l与圆C相切,求l的方程;
(2)若l与圆C相交于P、Q两点,若|PQ|=2 ![]() ,求此时直线l的方程.
,求此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在长方体ABCD﹣A1B1C1D1中,BC=2AB=4, ![]() ,E是A1D1的中点.
,E是A1D1的中点.
(Ⅰ)在平面A1B1C1D1内,请作出过点E与CE垂直的直线l,并证明l⊥CE;
(Ⅱ)设(Ⅰ)中所作直线l与CE确定的平面为α,求点C1到平面α的距离.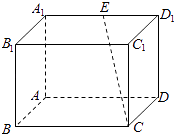
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义函数序列: ![]() ,f2(x)=f(f1(x)),f3(x)=f(f2(x)),…,fn(x)=f(fn﹣1(x)),则函数y=f2017(x)的图像与曲线
,f2(x)=f(f1(x)),f3(x)=f(f2(x)),…,fn(x)=f(fn﹣1(x)),则函数y=f2017(x)的图像与曲线 ![]() 的交点坐标为( )
的交点坐标为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com