
已知函数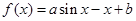 (
(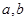 均为正常数),设函数
均为正常数),设函数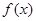 在
在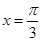 处有极值.
处有极值.
(1)若对任意的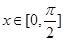 ,不等式
,不等式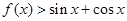 总成立,求实数
总成立,求实数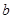 的取值范围;
的取值范围;
(2)若函数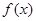 在区间
在区间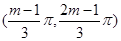 上单调递增,求实数
上单调递增,求实数 的取值范围.
的取值范围.
(1)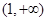 ;(2)
;(2)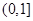 .
.
解析试题分析:本题主要考查导数的应用、不等式、三角函数等基础知识,考查思维能力、运算能力、分析问题与解决问题的能力,考查函数思想、转化思想等数学思想方法.第一问,对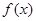 求导,因为
求导,因为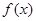 在
在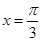 有极值,所以
有极值,所以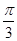 是
是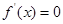 的根,列出表达式,求出
的根,列出表达式,求出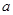 ,不等式恒成立等价于
,不等式恒成立等价于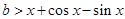 恒成立,所以下面的主要任务是求
恒成立,所以下面的主要任务是求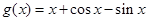 的最大值,对
的最大值,对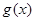 求导,利用三角公式化简,求
求导,利用三角公式化简,求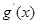 的最值,判断
的最值,判断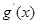 的正负,从而判断
的正负,从而判断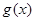 的单调性,求出最大值;第二问,由
的单调性,求出最大值;第二问,由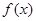 单调递增,所以
单调递增,所以 解出
解出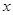 的取值范围,由已知
的取值范围,由已知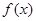 在
在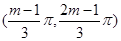 上单调递增,所以得出
上单调递增,所以得出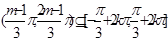 ,利用子集关系列出不等式组,解出
,利用子集关系列出不等式组,解出 .
.
试题解析:∵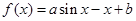 ,∴
,∴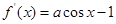 ,
,
由题意,得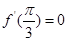 ,
,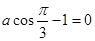 ,解得
,解得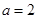 . 2分
. 2分
(1)不等式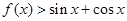 等价于
等价于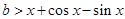 对于一切
对于一切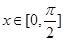 恒成立. 4分
恒成立. 4分
记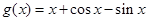
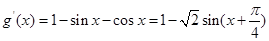 5分
5分
∵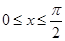 ,∴
,∴ ,∴
,∴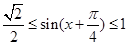 ,∴
,∴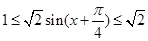 ,
,
∴ ,从而
,从而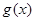 在
在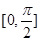 上是减函数.
上是减函数.
∴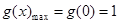 ,于是
,于是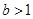 ,故
,故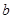 的取值范围是
的取值范围是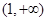 . 6分
. 6分
(2)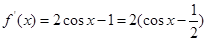 ,由
,由 ,得
,得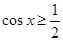 ,即
,即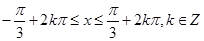 . 7分
. 7分
∵函数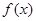 在区间
在区间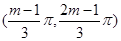 上单调递增,
上单调递增,
∴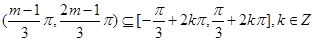 ,
,
则有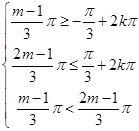 ,
, , 9分
, 9分
即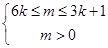 ,
, ,
,
∴只有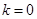 时,
时,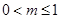 适合题意,故
适合题意,故 的取值范围为
的取值范围为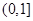 . 12分
. 12分
考点:1.导数的运算;2.两角和的正弦公式;3.三角函数的最值;4.恒成立问题;5.利用导数判断函数的单调性.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案科目:高中数学 来源: 题型:解答题
设函数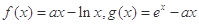 ,其中a为正实数.
,其中a为正实数.
(l)若x=0是函数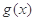 的极值点,讨论函数
的极值点,讨论函数 的单调性;
的单调性;
(2)若 在
在 上无最小值,且
上无最小值,且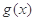 在
在 上是单调增函数,求a的取值范
上是单调增函数,求a的取值范
围;并由此判断曲线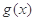 与曲线
与曲线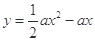 在
在 交点个数.
交点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数
(1)当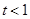 时,求函数
时,求函数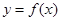 的单调区间;
的单调区间;
(2)当函数自变量的取值区间与对应函数值的取值区间相同时,这样的区间称为函数的保值区间。设 ,试问函数
,试问函数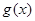 在
在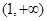 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com