
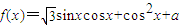
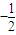 ,当
,当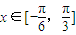 时,函数f(x)的最大值与最小值的和为
时,函数f(x)的最大值与最小值的和为 .
. ,求出字母系数a,在坐标系中用五点法做出函数的图象,坐标系的几个元素不要忽略.
,求出字母系数a,在坐标系中用五点法做出函数的图象,坐标系的几个元素不要忽略.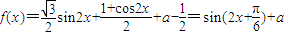 ,
,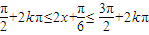 ,
,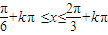 k∈z
k∈z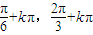 ]k∈z.
]k∈z.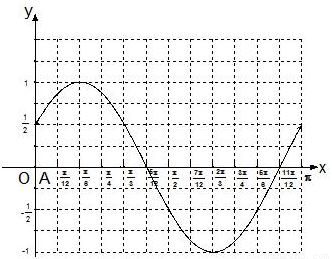 (II)∵-
(II)∵-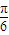 ≤x
≤x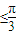 ,
,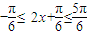 ,
,
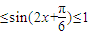
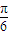 ,
,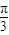 ]时,
]时,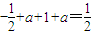 ,
,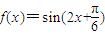 ,图象如图.
,图象如图.

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
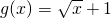 ,函数
,函数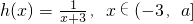 ,其中a为常数且a>0,令函数f(x)=g(x)•h(x).
,其中a为常数且a>0,令函数f(x)=g(x)•h(x). 时,求函数f(x)的值域;
时,求函数f(x)的值域; ?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.
?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.查看答案和解析>>
科目:高中数学 来源:2006年上海市普陀区高考数学一模试卷(解析版) 题型:解答题
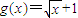 ,函数
,函数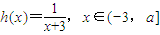 ,其中a为常数且a>0,令函数f(x)=g(x)•h(x).
,其中a为常数且a>0,令函数f(x)=g(x)•h(x).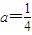 时,求函数f(x)的值域;
时,求函数f(x)的值域;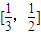 ?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.
?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.查看答案和解析>>
科目:高中数学 来源:2010年辽宁省沈阳市高考数学三模试卷(理科)(解析版) 题型:解答题
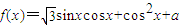
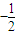 ,当
,当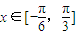 时,函数f(x)的最大值与最小值的和为
时,函数f(x)的最大值与最小值的和为 .
.查看答案和解析>>
科目:高中数学 来源:2011年高三数学单元检测:三角函数(1)(解析版) 题型:解答题
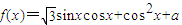
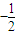 ,当
,当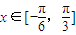 时,函数f(x)的最大值与最小值的和为
时,函数f(x)的最大值与最小值的和为 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com