
 及OB上,∠OMN=90°),且沿湖边修建休闲走廊.现甲部门需要人造湖的面积最大,乙部门需要走廊最长.请你设计一个方案,该方案( )
及OB上,∠OMN=90°),且沿湖边修建休闲走廊.现甲部门需要人造湖的面积最大,乙部门需要走廊最长.请你设计一个方案,该方案( )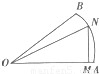
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
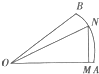
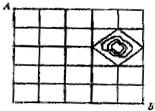 15、如图所示,某城镇由6条东西方向的街道和6条南北方向的街道组成,其中有一个池塘,街道在此变成一个菱形的环池大道,现要从城镇的A处走到B处,使所走的路程最短,最多可以有
15、如图所示,某城镇由6条东西方向的街道和6条南北方向的街道组成,其中有一个池塘,街道在此变成一个菱形的环池大道,现要从城镇的A处走到B处,使所走的路程最短,最多可以有
查看答案和解析>>
科目:高中数学 来源: 题型:
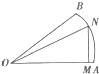 如图所示,某城镇为适应旅游产业的需要,欲在一扇形OAB(其中∠AOB=45°,扇形半径为1)草地上修建一个三角形人造湖OMN(其中M在OA上,N在
如图所示,某城镇为适应旅游产业的需要,欲在一扇形OAB(其中∠AOB=45°,扇形半径为1)草地上修建一个三角形人造湖OMN(其中M在OA上,N在 |
| AB |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
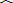 |
| AB |
| A.只能满足甲部门,不能满足乙部门 |
| B.只能满足乙部门,不能满足甲部门 |
| C.可以同时满足两个部门 |
| D.两个部门都不能满足 |
查看答案和解析>>
科目:高中数学 来源:2010年江西省南昌市新建二中高考数学二模试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com