
【题目】已知数列{an}的首项a1=1,且an+1=2an+1(n∈N*)
(Ⅰ)证明数列{an+1}是等比数列,并求数列{an}的通项公式;
(Ⅱ)设bn= ![]() ,求数列{bn}的前n项和Sn;
,求数列{bn}的前n项和Sn;
(Ⅲ)在条件(Ⅱ)下对任意正整数n,不等式Sn+ ![]() ﹣1>(﹣1)na恒成立,求实数a的取值范围.
﹣1>(﹣1)na恒成立,求实数a的取值范围.
【答案】证明:(I)∵an+1=2an+1(n∈N*),∴an+1+1=2(an+1),
∴数列{an+1}是等比数列,首项为2,公比为2.
∴an+1=2n,解得an=2n﹣1.
解:(Ⅱ)bn= ![]() =
= ![]() ,
,
数列{bn}的前n项和Sn= ![]() +…+
+…+ ![]() ,
,
∴ ![]() =
= ![]() +…+
+…+ ![]() +
+ ![]() ,
,
相减可得: ![]() =
= ![]() +…+
+…+ ![]() ﹣﹣
﹣﹣ ![]() =
= ![]() ﹣
﹣ ![]() ,
,
可得:Sn=2﹣ ![]() .
.
(Ⅲ)在条件(Ⅱ)下对任意正整数n,不等式Sn+ ![]() ﹣1>(﹣1)na,
﹣1>(﹣1)na,
化为:(﹣1)na<1﹣ ![]() .
.
n为奇数时,a>﹣ ![]() ,可得a>﹣
,可得a>﹣ ![]() .
.
n为偶数时,a<1﹣ ![]() .可得a
.可得a ![]() .
.
∵对任意正整数n,不等式Sn+ ![]() ﹣1>(﹣1)na恒成立,
﹣1>(﹣1)na恒成立,
∴ ![]() .
.
∴实数a的取值范围是 ![]() .
.
【解析】()(1)由an+1=2an+1(n∈N*),∴an+1+1=2(an+1),即可得出数列{an+1}是等比数列,根据等比数列的通项公式,从而得到an的通项公式,(2)由(1)中an的通项公式表示出bn,通过错位相减可求得数列{bn}的前n项和Sn,(3)在(2)的条件下,不等式Sn+![]() ﹣1>(-1)na,可化为:(﹣1)na<1﹣
﹣1>(-1)na,可化为:(﹣1)na<1﹣ ![]() ,对a进行分类讨论,可得到实数a的取值范围.
,对a进行分类讨论,可得到实数a的取值范围.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系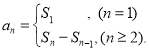 ,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的右焦点为F2(1,0),点P(1,
=1(a>b>0)的右焦点为F2(1,0),点P(1, ![]() )在椭圆C上.
)在椭圆C上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过坐标原点O的两条直线EF,MN分别与椭圆C交于E,F,M,N四点,且直线OE,OM的斜率之积为﹣ ![]() ,求证:四边形EMFN的面积为定值.
,求证:四边形EMFN的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直角梯形ABCD与等边△ABE所在的平面互相垂直,AB∥CD,AB⊥BC,AB=2CD=AD=2,F为线段EA上的点,且EA=3EF. 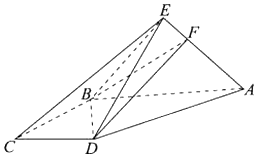
(I)求证:EC∥平面FBD
(Ⅱ)求多面体EFBCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设x∈R,记不超过x的最大整数为[x],例如[2.34]=2,[﹣1.5]=﹣2,令{x}=x﹣[x],则 ![]() ( )
( )
A.是等差数列但不是等比数列
B.既是等差数列也是等比数列
C.是等比数列但不是等差数列
D.既不是等差数列也不是等比数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x2+(2﹣m)x﹣m,g(x)=x2﹣x+2m.
(1)若m=1,求不等式f(x)>0的解集;
(2)若m>0,求关于x的不等式f(x)≤g(x)的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com