
【题目】已知函数f(x)=loga(![]() )(0<a<1,b>0)为奇函数,当x∈(﹣1,a]时,函数y=f(x)的值域是(﹣∞,1].
)(0<a<1,b>0)为奇函数,当x∈(﹣1,a]时,函数y=f(x)的值域是(﹣∞,1].
(1)确定b的值;
(2)证明函数y=f(x)在定义域上单调递增,并求a的值;
(3)若对于任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)>0恒成立,求k的取值范围.
【答案】(1)b=1;(2)见解析;(3)![]()
【解析】
(1)利用f(﹣x)+f(x)=0求出b的值.(2)利用函数单调性的定义证明函数y=f(x)在定义域上单调递增,再利用y=f(x)的值域是(﹣∞,1]求出a的值.(3)首先转化为t2﹣2t>k﹣2t2,再转化为k<3t2﹣2t的最小值,求3t2﹣2t的最小值即得解.
(1)∵函数f(x)=loga(![]() )(0<a<1,b>0)为奇函数,
)(0<a<1,b>0)为奇函数,
∴f(﹣x)=﹣f(x),即f(﹣x)+f(x)=0,
∴loga![]() +loga
+loga![]() =loga(
=loga(![]()
![]() )=0,即
)=0,即![]()
![]() =1,
=1,
∴1﹣x2=b2﹣x2,即b2=1,解得b=1(﹣1舍去),
当b=1时,函数f(x)=loga![]() 为奇函数,满足条件.
为奇函数,满足条件.
(2)证明:设x1,x2∈(﹣1,1),且x1<x2,由g(x)=![]() =﹣1+
=﹣1+![]() ,
,
g(x1)﹣g(x2)=![]() ,
,
x1,x2∈(﹣1,1),且x1<x2,可得x2﹣x1>0,(1+x1)(1+x2)>0,
则g(x1)﹣g(x2)>0,即有g(x)在(﹣1,1)递减,
由f(x)=logag(x),0<a<1可得,
f(x)在(﹣1,1)递增;
∴函数f(x)=loga![]() 在x∈(﹣1,a)上单调递增,
在x∈(﹣1,a)上单调递增,
∵当x∈(﹣1,a]时,函数f(x)的值域是(﹣∞,1],
∴f(a)=1,即f(a)=loga![]() =1,∴
=1,∴![]() =a,
=a,
即1﹣a=a+a2,∴a2+2a﹣1=0,解得a=﹣1±![]() ,∵0<a<1,∴a=﹣1+
,∵0<a<1,∴a=﹣1+![]() ;
;
(3)对于任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)>0恒成立,
即有f(t2﹣2t)>﹣f(2t2﹣k)=f(k﹣2t2),
由f(x)在(﹣1,1)递增,
可得k<3t2﹣2t的最小值,
由3t2﹣2t=3(t﹣![]() )2﹣
)2﹣![]() ,可得t=
,可得t=![]() ,取得最小值﹣
,取得最小值﹣![]() ,可得k<﹣
,可得k<﹣![]() .检验成立.
.检验成立.
则k的取值范围是(﹣∞,﹣![]() ).
).


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
【题目】数学家欧拉在1765年提出,任意三角形的外心、重心、垂心位于同一条直线上,后人称这条直线为欧拉线.已知△ABC的顶点A(2,0),B(0,4),若其欧拉线的方程为x-y+2=0,则顶点C的坐标为
A. (-4,0) B. (-3,-1) C. (-5,0) D. (-4,-2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() 、
、![]() ,
,![]() 为椭圆
为椭圆![]() 的一个短轴顶点,
的一个短轴顶点,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若经过椭圆![]() 左焦点的直线
左焦点的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,
两点,![]() 为椭圆
为椭圆![]() 的右顶点,求
的右顶点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象经过点(
的图象经过点(![]() ,
,![]() )和(
)和(![]() ,
,![]() ),完成下面问题:
),完成下面问题:

(1)求函数![]() 的表达式;
的表达式;
(2)在给出的平面直角坐标系中,请用适当的方法画出这个函数的图象,并写出这个函数的一条性质;
(3)已知函数![]() 的图象如图所示,结合你所画出
的图象如图所示,结合你所画出![]() 的图象,直接写出
的图象,直接写出![]() 的解集.
的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数y=﹣x2+2|x|+1的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | ﹣2 |
| m | 2 | 1 | 2 | 1 |
| ﹣2 | … |
其中,m= .
(2)根据上表数据,在如图所示的平面直角坐标系中描点,画出了函数图象的一部分,请画出该函数图象的另一部分.
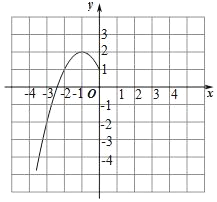
(3)观察函数图象,写出两条函数的性质./p>
(4)进一步探究函数图象发现:
①方程﹣x2+2|x|+1=0有 个实数根;
②关于x的方程﹣x2+2|x|+1=a有4个实数根时,a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了整顿道路交通秩序,某地考虑对行人闯红灯进行处罚.为了更好地了解市民的态度,在普通人中随机抽取200人进行调查,当不处罚时,有80人会闯红灯,处罚时,得到如下数据:
处罚金额 | 5 | 10 | 15 | 20 |
会闯红灯的人数 | 50 | 40 | 20 | 0 |
若用表中数据所得频率代替概率.
(1)当处罚金定为10元时,行人闯红灯的概率会比不进行处罚降低多少?
(2)将选取的200人中会闯红灯的市民分为两类:![]() 类市民在罚金不超过10元时就会改正行为;
类市民在罚金不超过10元时就会改正行为;![]() 类是其它市民.现对
类是其它市民.现对![]() 类与
类与![]() 类市民按分层抽样的方法抽取4人依次进行深度问卷,则前两位均为
类市民按分层抽样的方法抽取4人依次进行深度问卷,则前两位均为![]() 类市民的概率是多少?
类市民的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】调查机构对某高科技行业进行调查统计,得到该行业从业者学历分布扇形图和从事该行业岗位分布条形图,如图所示,判断以下三种说法的正误:①该高科技行业从业人员中学历为博士的占一半以上;②该高科技行业中从事技术岗位的人数超过总数的30%;③该高科技行业中从事运营岗位的人员主要是本科生.


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某部影片的盈利额(即影片的票房收入与固定成本之差)记为![]() ,观影人数记为
,观影人数记为![]() ,其函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后
,其函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后![]() 与
与![]() 的函数图象.
的函数图象.

给出下列四种说法:
①图(2)对应的方案是:提高票价,并提高成本;
②图(2)对应的方案是:保持票价不变,并降低成本;
③图(3)对应的方案是:提高票价,并保持成本不变;
④图(3)对应的方案是:提高票价,并降低成本.
其中,正确的说法是____________.(填写所有正确说法的编号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com