
【题目】有甲、乙两家外卖公司,其送餐员的日工资方案如下:甲公司底薪![]() 元,送餐员每单制成
元,送餐员每单制成![]() 元;乙公司无底薪,
元;乙公司无底薪,![]() 单以内(含
单以内(含![]() 单)的部分送餐员每单抽成
单)的部分送餐员每单抽成![]() 元,超过
元,超过![]() 单的部分送餐员每单抽成
单的部分送餐员每单抽成![]() 元.现从这两家公司各随机选取一名送餐员,分别记录其
元.现从这两家公司各随机选取一名送餐员,分别记录其![]() 天的送餐单数,得到如下频数分布表:
天的送餐单数,得到如下频数分布表:
送餐单数 | 38 | 39 | 40 | 41 | 42 |
甲公司天数 | 10 | 10 | 15 | 10 | 5 |
乙公司天数 | 10 | 15 | 10 | 10 | 5 |
(1)从记录甲公司的![]() 天送餐单数中随机抽取
天送餐单数中随机抽取![]() 天,求这
天,求这![]() 天的送餐单数都不小于
天的送餐单数都不小于![]() 单的概率;
单的概率;
(2)假设同一公司的送餐员一天的送餐单数相同,将频率视为概率,回答下列两个问题:
①求乙公司送餐员日工资的分布列和数学期望;
②小张打算到甲、乙两家公司中的一家应聘送餐员,如果仅从日工资的角度考虑,小张应选择哪家公司应聘?明你的理由.
【答案】(1)![]() ;(2)①分布列见解析,
;(2)①分布列见解析,![]() ;②小张应选择甲公司应聘.
;②小张应选择甲公司应聘.
【解析】
(1)记抽取的3天送餐单数都不小于40为事件![]() ,可得
,可得![]() (A)的值.
(A)的值.
(2)①设乙公司送餐员送餐单数为![]() ,可得当
,可得当![]() 时,
时,![]() ,以此类推可得:当
,以此类推可得:当![]() 时,当
时,当![]() 时,
时,![]() 的值.当
的值.当![]() 时,
时,![]() 的值,同理可得:当
的值,同理可得:当![]() 时,
时,![]() .
.![]() 的所有可能取值.可得
的所有可能取值.可得![]() 的分布列及其数学期望.
的分布列及其数学期望.
②依题意,甲公司送餐员日平均送餐单数.可得甲公司送餐员日平均工资,与乙数学期望比较即可得出.
解:(1)由表知,50天送餐单数中有30天的送餐单数不小于40单,
记抽取的3天送餐单数都不小于40为事件![]() ,
,
则![]() .
.
(2)①设乙公司送餐员的送餐单数为![]() ,日工资为
,日工资为![]() 元,则
元,则
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以![]() 的分布列为
的分布列为
| 228 | 234 | 240 | 247 | 254 |
|
|
|
|
|
|
![]() .
.
②依题意,甲公司送餐员的日平均送餐单数为
![]() ,
,
所以甲公司送餐员的日平均工资为![]() 元,
元,
因为![]() ,所以小张应选择甲公司应聘.
,所以小张应选择甲公司应聘.


 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案科目:高中数学 来源: 题型:
【题目】随着时代的发展,A城市的竞争力、影响力日益卓著,这座创新引领型城市有望踏上向“全球城市”发起“冲击”的新征程.A城市的活力与包容无不吸引着无数怀揣梦想的年轻人前来发展,目前A城市的常住人口大约为1300万.近日,某报社记者作了有关“你来A城市发展的理由”的调查问卷,参与调查的对象年龄层次在25~44岁之间.收集到的相关数据如下:
来A城市发展的理由 | 人数 | 合计 | |
自然环境 | 1.森林城市,空气清新 | 200 | 300 |
2.降水充足,气候怡人 | 100 | ||
人文环境 | 3.城市服务到位 | 150 | 700 |
4.创业氛围好 | 300 | ||
5.开放且包容 | 250 | ||
合计 | 1000 | 1000 | |
(1)根据以上数据,预测400万25~44岁年龄的人中,选择“创业氛围好”来A城市发展的有多少人;
(2)从所抽取选择“自然环境”作为来A城市发展的理由的300人中,利用分层抽样的方法抽取6人,从这6人中再选取3人发放纪念品.求选出的3人中至少有2人选择“森林城市,空气清新”的概率;
(3)在选择“自然环境”作为来A城市发展的理由的300人中有100名男性;在选择“人文环境”作为来A城市发展的理由的700人中有400名男性;请填写下面![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为性别与“自然环境”或“人文环境”的选择有关?
的把握认为性别与“自然环境”或“人文环境”的选择有关?
自然环境 | 人文环境 | 合计 | |
男 | |||
女 | |||
合计 |
附: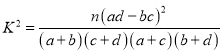 ,
,![]() .
.
P( | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买每满![]() 元的商品即可抽奖一次.抽奖规则如下:抽奖者掷各面标有
元的商品即可抽奖一次.抽奖规则如下:抽奖者掷各面标有![]() 点数的正方体骰子
点数的正方体骰子![]() 次,若掷得点数大于
次,若掷得点数大于![]() ,则可继续在抽奖箱中抽奖;否则获得三等奖,结束抽奖,已知抽奖箱中装有
,则可继续在抽奖箱中抽奖;否则获得三等奖,结束抽奖,已知抽奖箱中装有![]() 个红球与
个红球与![]() 个白球,抽奖者从箱中任意摸出
个白球,抽奖者从箱中任意摸出![]() 个球,若
个球,若![]() 个球均为红球,则获得一等奖,若
个球均为红球,则获得一等奖,若![]() 个球为
个球为![]() 个红球和
个红球和![]() 个白球,则获得二等奖,否则,获得三等奖(抽奖箱中的所有小球,除颜色外均相同).
个白球,则获得二等奖,否则,获得三等奖(抽奖箱中的所有小球,除颜色外均相同).
![]() 若
若![]() ,求顾客参加一次抽奖活动获得三等奖的概率;
,求顾客参加一次抽奖活动获得三等奖的概率;
![]() 若一等奖可获奖金
若一等奖可获奖金![]() 元,二等奖可获奖金
元,二等奖可获奖金![]() 元,三等奖可获奖金
元,三等奖可获奖金![]() 元,记顾客一次抽奖所获得的奖金为
元,记顾客一次抽奖所获得的奖金为![]() ,若商场希望
,若商场希望![]() 的数学期望不超过
的数学期望不超过![]() 元,求
元,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() 、
、![]() ,直线
,直线![]() 、
、![]() 相交于点
相交于点![]() ,且它们的斜率之积为
,且它们的斜率之积为![]() ,记动点
,记动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)已知定点![]() ,
,![]() ,过点
,过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点 ,则直线
两点 ,则直线![]() 与
与![]() 斜率之积是否为定值,若是求出定值;若不是请说明理由.
斜率之积是否为定值,若是求出定值;若不是请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两班各派三名同学参加知识竞赛,每人回答一个问题,答对得10分,答错得0分,假设甲班三名同学答对的概率都是![]() ,乙班三名同学答对的概率分别是
,乙班三名同学答对的概率分别是![]() ,
,![]() ,
,![]() ,且这六名同学答题正确与否相互之间没有影响.
,且这六名同学答题正确与否相互之间没有影响.
(1)记“甲、乙两班总得分之和是60分”为事件![]() ,求事件
,求事件![]() 发生的概率;
发生的概率;
(2)用![]() 表示甲班总得分,求随机变量
表示甲班总得分,求随机变量![]() 的概率分布和数学期望.
的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
平面直角坐标系xOy中,曲线C:![]() .直线l经过点P(m,0),且倾斜角为
.直线l经过点P(m,0),且倾斜角为![]() .O为极点,以x轴正半轴为极轴,建立极坐标系.
.O为极点,以x轴正半轴为极轴,建立极坐标系.
(Ⅰ)写出曲线C的极坐标方程与直线l的参数方程;
(Ⅱ)若直线l与曲线C相交于A,B两点,且|PA|·|PB|=1,求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com