
【题目】如图,圆![]() 的圆心在
的圆心在![]() 轴上,且过点
轴上,且过点![]() ,
,![]() .
.
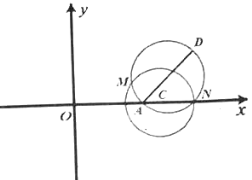
(1)求圆![]() 的方程;
的方程;
(2)直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为直线
为直线![]() 上位于第一象限内的一点,以
上位于第一象限内的一点,以![]() 为直径的圆与圆
为直径的圆与圆![]() 相交于点
相交于点![]() ,
,![]() .若直线
.若直线![]() 的斜率为-2,求
的斜率为-2,求![]() 点坐标.
点坐标.
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,直线
,直线![]() 与E交于A、B两点,且
与E交于A、B两点,且![]() ,其中O为原点.
,其中O为原点.
(1)求抛物线E的方程;
(2)点C坐标为![]() ,记直线CA、CB的斜率分别为
,记直线CA、CB的斜率分别为![]() ,证明:
,证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且(c﹣2a) ![]() =c
=c ![]()
![]()
(1)求B的大小;
(2)已知f(x)=cosx(asinx﹣2cosx)+1,若对任意的x∈R,都有f(x)≤f(B),求函数f(x)的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=2![]() cos
cos![]() ,直线l的参数方程为
,直线l的参数方程为![]() (t为参数),直线l与圆C交于A,B两点,P是圆C上不同于A,B的任意一点.
(t为参数),直线l与圆C交于A,B两点,P是圆C上不同于A,B的任意一点.
(1)求圆心的极坐标;
(2)求△PAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学成就的杰出代表.其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积![]() .弧田,由圆弧和其所对的弦所围成.公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,按照上述经验公式计算所得弧田面积与实际面积之间存在误差.现有圆心角为
.弧田,由圆弧和其所对的弦所围成.公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,按照上述经验公式计算所得弧田面积与实际面积之间存在误差.现有圆心角为![]() ,弦长等于
,弦长等于![]() 米的弧田. 按照上述经验公式计算所得弧田面积与实际面积的误差为_______平方米.(用“实际面积减去弧田面积”计算)
米的弧田. 按照上述经验公式计算所得弧田面积与实际面积的误差为_______平方米.(用“实际面积减去弧田面积”计算)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据下列对几何体结构特征的描述,说出几何体的名称.
(1)由八个面围成,其中两个面是互相平行且全等的正六边形,其它各面都是矩形;
(2)一个等腰梯形绕着两底边中点的连线所在的直线旋转180°形成的封闭曲面所围成的几何体;
(3)由五个面围成,其中一个面是正方形,其他各面都是有一个公共顶点的全等三角形;
(4)一个圆绕其一条直径所在的直线旋转180°形成的封闭曲面所围成的几何体.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 三边是连续的三个自然数.
三边是连续的三个自然数.
(Ⅰ)求最小边的取值范围;
(Ⅱ)是否存在这样的![]() ,使得其最大内角是最小内角的两倍?若存在,试求出这个三角形的三边;若不存在,请说明理由.
,使得其最大内角是最小内角的两倍?若存在,试求出这个三角形的三边;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校从参加高一年级期中考试的学生中抽出![]() 名学生,并统计了她们的数学成绩(成绩均为整数且满分为
名学生,并统计了她们的数学成绩(成绩均为整数且满分为![]() 分),数学成绩分组及各组频数如下:
分),数学成绩分组及各组频数如下:
![]()
样本频率分布表:
分组 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
(1)在给出的样本频率分布表中,求![]() 的值;
的值;
(2)估计成绩在![]() 分以上(含
分以上(含![]() 分)学生的比例;
分)学生的比例;
(3)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩在![]() 的学生中选两位同学,共同帮助成绩在
的学生中选两位同学,共同帮助成绩在![]() 中的某一位同学.已知甲同学的成绩为
中的某一位同学.已知甲同学的成绩为![]() 分,乙同学的成绩为
分,乙同学的成绩为![]() 分,求甲、乙两同学恰好被安排在同一小组的概率.
分,求甲、乙两同学恰好被安排在同一小组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com