
【题目】已知函数f(x)=xe2x﹣lnx﹣ax.
(1)当a=0时,求函数f(x)在[ ![]() ,1]上的最小值;
,1]上的最小值;
(2)若x>0,不等式f(x)≥1恒成立,求a的取值范围;
(3)若x>0,不等式f( ![]() )﹣1≥
)﹣1≥ ![]() e
e ![]() +
+ ![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
【答案】
(1)解:a=0时,f(x)=xe2x﹣lnx,
∴ ![]() ,
, ![]() ,
,
∴函数f′(x)在(0,+∞)上是增函数,
又函数f′(x)的值域为R,
故x0>0,使得f′(x0)=(2x0+1)e ![]() ﹣
﹣ ![]() =0,
=0,
又∵ ![]() ,∴
,∴ ![]() ,∴当x∈[
,∴当x∈[ ![]() ,1]时,f′(x)>0,
,1]时,f′(x)>0,
即函数f(x)在区间[ ![]() ,1]上递增,∴
,1]上递增,∴ ![]()
(2)解: ![]() ,
,
由(1)知函数f′(x)在(0,+∞)上是增函数,且x0>0,使得f′(x0)=0,
进而函数f(x)在区间(0,x0)上递减,在(x0,+∞)上递增,
![]() ﹣lnx0﹣ax0,
﹣lnx0﹣ax0,
由f′(x0)=0,得:(2x0+1)e ![]() ﹣
﹣ ![]() ﹣a=0,
﹣a=0,
∴ ![]() ,∴f(x0)=1﹣lnx0﹣2x02
,∴f(x0)=1﹣lnx0﹣2x02 ![]() ,
,
∵x>0,不等式f(x)≥1恒成立,
∴1﹣lnx0﹣2x02e ![]() ≥1,∴lnx0+2x02
≥1,∴lnx0+2x02 ![]() ≤0,
≤0,
设h(x0)=lnx0+2x ![]() e
e ![]() ,则h(x0)为增函数,且有唯一零点,设为t,
,则h(x0)为增函数,且有唯一零点,设为t,
则h(t)=lnt+2t2e2t=0,则﹣lnt=2t2e2t,即 ![]() ,
,
令g(x)=xex,则g(x)单调递增,且g(2t)=g( ![]() ),
),
则2t=ln ![]() ,即
,即 ![]() ,
,
∵a=(2x0+1) ![]() ﹣
﹣ ![]() 在(0,t]为增函数,
在(0,t]为增函数,
则当x0=t时,a有最大值, ![]() =
= ![]() ,
,
∴a≤2,∴a的取值范围是(﹣∞,2]
(3)解:由f( ![]() )﹣1≥
)﹣1≥ 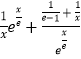 ,
,
得  ,
,
∴xlnx﹣x﹣a≥ ![]() ,∴a
,∴a 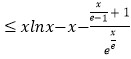 对任意x>0成立,
对任意x>0成立,
令函数g(x)=xlnx﹣x﹣ ![]() ,∴
,∴ ![]() ,
,
当x>1时,g′(x)>0,当0<x<1时,g′(x)<0,
∴当x=1时,函数g(x)取得最小值g(1)=﹣1﹣ ![]() =﹣1﹣
=﹣1﹣ ![]() ,
,
∴a≤﹣1﹣ ![]() .
.
∴a的取值范围是(﹣∞,﹣1﹣ ![]() )
)
【解析】(1)a=0时, ![]() ,
, ![]() ,由此利用导数性质能求出函数f(x)在[
,由此利用导数性质能求出函数f(x)在[ ![]() ,1]上的最小值.(2)
,1]上的最小值.(2) ![]() ,函数f(x)在区间(0,x0)上递减,在(x0 , +∞)上递增,由x>0,不等式f(x)≥1恒成立,得lnx0+2x02
,函数f(x)在区间(0,x0)上递减,在(x0 , +∞)上递增,由x>0,不等式f(x)≥1恒成立,得lnx0+2x02 ![]() ≤0,由此能求出a的取值范围.(3)由f(
≤0,由此能求出a的取值范围.(3)由f( ![]() )﹣1≥
)﹣1≥ 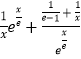 ,得a
,得a 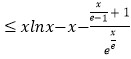 对任意x>0成立,令函数g(x)=xlnx﹣x﹣
对任意x>0成立,令函数g(x)=xlnx﹣x﹣ ![]() ,则
,则 ![]() ,由此利用导数性质能求出a的取值范围.
,由此利用导数性质能求出a的取值范围.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】第35届牡丹花会期间,我班有5名学生参加志愿者服务,服务场所是王城公园和牡丹公园.
(1)若学生甲和乙必须在同一个公园,且甲和丙不能在同一个公园,则共有多少种不同的分配方案?
(2)每名学生都被随机分配到其中的一个公园,设X,Y分别表示5名学生分配到王城公园和牡丹公园的人数,记ξ=|X﹣Y|,求随机变量ξ的分布列和数学期望E(ξ)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计划在某水库建一座至多安装 ![]() 台发电机的水电站,过去
台发电机的水电站,过去 ![]() 年的水文资料显示,水库年入流量
年的水文资料显示,水库年入流量 ![]() (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,不足
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,不足 ![]() 的年份有
的年份有 ![]() 年,不低于
年,不低于 ![]() 且不超过
且不超过 ![]() 的年份有
的年份有 ![]() 年,超过
年,超过 ![]() 的年份有
的年份有 ![]() 年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
(1)求未来 ![]() 年中,设
年中,设 ![]() 表示流量超过
表示流量超过 ![]() 的年数,求
的年数,求 ![]() 的分布列及期望;
的分布列及期望;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量 ![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电机最多可运行台数 | 1 |
|
|
若某台发电机运行,则该台年利润为 ![]() 万元,若某台发电机未运行,则该台年亏损
万元,若某台发电机未运行,则该台年亏损 ![]() 万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解青少年的肥胖是否与常喝碳酸饮料有关,现对30名青少年进行调查,得到如下列联表:
常喝 | 不常喝 | 总计 | |
肥胖 | 2 | ||
不肥胖 | 18 | ||
总计 | 30 |
已知从这30名青少年中随机抽取1名,抽到肥胖青少年的概率为 ![]() .
.
(1)请将列联表补充完整;
(2)是否有99.5%的把握认为青少年的肥胖与常喝碳酸饮料有关?
独立性检验临界值表:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: ![]() ,其中n=a+b+c+d .
,其中n=a+b+c+d .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,设椭圆 ![]() =1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.
=1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.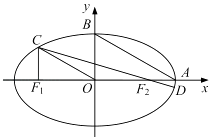
(1)若OC∥AB,求e的值;
(2)连结CF2并延长交椭圆于另一点D若 ![]() ≤e≤
≤e≤ ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理过程是演绎推理的是( )
A.某校高三(1)班有55人,2班有54人,3班有52人,由此得高三所有班人数超过50人
B.两条直线平行,同旁内角互补,如果∠A与∠B是两条平行直线的同旁内角,则∠A+∠B=180°
C.由平面三角形的性质,推测空间四边形的性质
D.在数列{an}中,a1=1,an= ![]() (an-1+
(an-1+ ![]() )(n≥2),由此归纳出{an}的通项公
)(n≥2),由此归纳出{an}的通项公
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位学生参加数学竞赛培训,在培训期间他们参加的5次预寒成绩记录如下:
甲:82,82,79,95,87
乙:95,75,80,90,85
(1)用茎叶图表示这两组数据;
(2)求甲、乙两人成绩的平均数与方差;
(3)若现要从中选派一人参加数学竞赛,你认为选派哪位学生参加合适,说明理由?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com