
【题目】已知椭圆![]() 的长轴长为
的长轴长为![]() ,焦距为2,抛物线
,焦距为2,抛物线![]() 的准线经过椭圆
的准线经过椭圆![]() 的左焦点
的左焦点![]() .
.
(1)求椭圆![]() 与抛物线
与抛物线![]() 的方程;
的方程;
(2)直线![]() 经过椭圆
经过椭圆![]() 的上顶点且
的上顶点且![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() ,
,![]() 与抛物线
与抛物线![]() 分别交于点
分别交于点![]() (异于点
(异于点![]() ),
),![]() (异于点
(异于点![]() ),证明:直线
),证明:直线![]() 的斜率为定值.
的斜率为定值.
【答案】(1)椭圆![]() 的方程为
的方程为![]() ,抛物线
,抛物线![]() 的方程为
的方程为![]() ;(2)见试题解析.
;(2)见试题解析.
【解析】
(1)由题意可得![]() ,
,![]() 的值,运用
的值,运用![]() ,求得
,求得![]() ,可得椭圆
,可得椭圆![]() 的方程.由抛物线
的方程.由抛物线![]() 的准线经过椭圆
的准线经过椭圆![]() 的左焦点
的左焦点![]() ,求得
,求得![]() ,即可得抛物线
,即可得抛物线![]() 的方程.
的方程.
(2)设直线![]() 的方程为
的方程为![]() ,与抛物线
,与抛物线![]() 的方程联立,消去
的方程联立,消去![]() ,可得
,可得![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() ,即
,即![]() ,
,![]() ,直线
,直线![]() 方程为
方程为![]() ,直线
,直线![]() 方程为
方程为![]() ,联立
,联立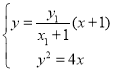 即
即![]() ,则
,则![]() ,
,![]() 为方程两根,解得
为方程两根,解得![]() ,同理
,同理![]() ,计算
,计算![]() 即可.
即可.
(1)由题意可知![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,![]()
![]() 椭圆
椭圆![]() 的方程为
的方程为![]()
![]() 抛物线
抛物线![]() 的准线经过椭圆
的准线经过椭圆![]() 的左焦点
的左焦点![]()
![]() 即
即![]()
抛物线![]() 的方程为
的方程为![]() .
.
(2)由题意可设直线![]() 的方程为
的方程为![]() ,
,
则![]() ,即
,即![]()
![]() 直线
直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点
两点
![]() ,解得
,解得![]() 且
且![]()
设![]() ,
,![]() ,
,![]() ,
,![]() 则
则![]() ,
,![]() 为方程
为方程![]() 的两根,即
的两根,即![]() ,
,![]()
直线![]() 方程为:
方程为:![]() ,直线
,直线![]() 方程为:
方程为:![]()
将直线![]() 方程与抛物线
方程与抛物线![]() 的方程联立
的方程联立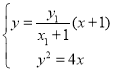
即![]() ,则
,则![]() 与
与![]() 是该方程两根.
是该方程两根.
所以 ,即
,即![]()
同理:直线![]() 方程为:
方程为:![]() 时
时![]()
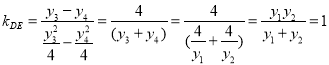
所以,直线![]() 的斜率为定值.
的斜率为定值.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】甲、乙、丙三个车床加工的零件分别为350个,700个,1050个,现用分层抽样的方法随机抽取6个零件进行检验.
(1)从抽取的6个零件中任意取出2个,已知这两个零件都不是甲车床加工的,求其中至少有一个是乙车床加工的零件;
(2)从抽取的6个零件中任意取出3个,记其中是乙车床加工的件数为X,求X的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,B,C分别是海岸线上的两个城市,两城市间由笔直的海滨公路相连,B,C之间的距离为100km,海岛A在城市B的正东方50![]() 处.从海岛A到城市C,先乘船按北偏西θ角(
处.从海岛A到城市C,先乘船按北偏西θ角(![]() ,其中锐角
,其中锐角![]() 的正切值为
的正切值为![]() )航行到海岸公路P处登陆,再换乘汽车到城市C.已知船速为25km/h,车速为75km/h.
)航行到海岸公路P处登陆,再换乘汽车到城市C.已知船速为25km/h,车速为75km/h.
(1)试建立由A经P到C所用时间与![]() 的函数解析式;
的函数解析式;
(2)试确定登陆点P的位置,使所用时间最少,并说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设曲线E的方程为![]() 1,动点A(m,n),B(﹣m,n),C(﹣m,﹣n),D(m,﹣n)在E上,对于结论:①四边形ABCD的面积的最小值为48;②四边形ABCD外接圆的面积的最小值为25π.下面说法正确的是( )
1,动点A(m,n),B(﹣m,n),C(﹣m,﹣n),D(m,﹣n)在E上,对于结论:①四边形ABCD的面积的最小值为48;②四边形ABCD外接圆的面积的最小值为25π.下面说法正确的是( )
A.①错,②对B.①对,②错C.①②都错D.①②都对
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年7月1日迎来了我国建党98周年,6名老党员在这天相约来到革命圣地之一的西柏坡.6名老党员中有3名党员当年在同一个班,他们站成一排拍照留念时,要求同班的3名党员站在一起,且满足条件的每种排法都要拍一张照片,若将照片洗出来,每张照片0.5元(不含过塑费),且有一半的照片需要过塑,每张过塑费为0.75元.若将这些照片平均分给每名老党员(过塑的照片也要平均分),则每名老党员需要支付的照片费为( )
A.20.5B.21元C.21.5元D.22元
查看答案和解析>>
科目:高中数学 来源: 题型:
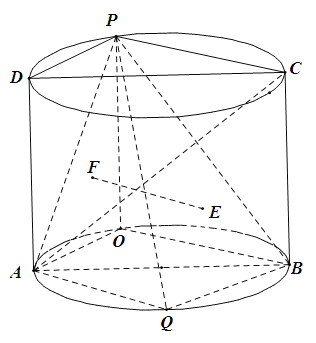
【题目】如图,圆柱的轴截面![]() 是边长为2的正方形,点
是边长为2的正方形,点![]() 是圆弧
是圆弧![]() 上的一动点(不与
上的一动点(不与![]() 重合),点
重合),点![]() 是圆弧
是圆弧![]() 的中点,且点
的中点,且点![]() 在平面
在平面![]() 的两侧.
的两侧.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)设点![]() 在平面
在平面![]() 上的射影为点
上的射影为点![]() ,点
,点![]() 分别是
分别是![]() 和
和![]() 的重心,当三棱锥
的重心,当三棱锥![]() 体积最大时,回答下列问题.
体积最大时,回答下列问题.
(ⅰ)证明:![]() 平面
平面![]() ;
;
(ⅱ)求平面![]() 与平面
与平面![]() 所成二面角的正弦值.
所成二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
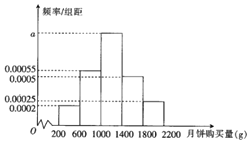
【题目】2018年中秋节到来之际,某超市为了解中秋节期间月饼的销售量,对其所在销售范围内的1000名消费者在中秋节期间的月饼购买量![]() 单位:
单位:![]() 进行了问卷调查,得到如下频率分布直方图:
进行了问卷调查,得到如下频率分布直方图:
![]() 求频率分布直方图中a的值;
求频率分布直方图中a的值;
![]() 以频率作为概率,试求消费者月饼购买量在
以频率作为概率,试求消费者月饼购买量在![]() 的概率;
的概率;
![]() 已知该超市所在销售范围内有20万人,并且该超市每年的销售份额约占该市场总量的
已知该超市所在销售范围内有20万人,并且该超市每年的销售份额约占该市场总量的![]() ,请根据这1000名消费者的人均月饼购买量估计该超市应准备多少吨月饼恰好能满足市场需求
,请根据这1000名消费者的人均月饼购买量估计该超市应准备多少吨月饼恰好能满足市场需求![]() 频率分布直方图中同一组的数据用该组区间的中点值作代表
频率分布直方图中同一组的数据用该组区间的中点值作代表![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为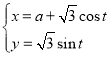 (
(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 上一点
上一点![]() 的极坐标为
的极坐标为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)设点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上(异于极点),若
上(异于极点),若![]() 四点依次在同一条直线
四点依次在同一条直线![]() 上,且
上,且![]() 成等比数列,求
成等比数列,求![]() 的极坐标方程.
的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保障全国第四次经济普查顺利进行,国家统计局从东部选择江苏, 从中部选择河北. 湖北,从西部选择宁夏, 从直辖市中选择重庆作为国家综合试点地区,然后再逐级确定普查区域,直到基层的普查小区.在普查过程中首先要进行宣传培训,然后确定对象,最后入户登记. 由于种种情况可能会导致入户登记不够顺利,这为正式普查提供了宝贵的试点经验. 在某普查小区,共有 50 家企事业单位,150 家个体经营户,普查情况如下表所示:
普查对象类别 | 顺利 | 不顺利 | 合计 |
企事业单位 | 40 | 10 | 50 |
个体经营户 | 100 | 50 | 150 |
合计 | 140 | 60 | 200 |
(1)写出选择 5 个国家综合试点地区采用的抽样方法;
(2)根据列联表判断是否有![]() 的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
(3)以频率作为概率, 某普查小组从该小区随机选择 1 家企事业单位,3 家个体经营户作为普查对象,入户登记顺利的对象数记为![]() , 写出
, 写出![]() 的分布列,并求
的分布列,并求![]() 的期望值.
的期望值.
附:![]()
| 0.10 | 0.010 | 0.001 |
| 2.706 | 6.635 | 10.88 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com