
如图所示的三棱锥A-BCD中,∠BAD=90°,AD⊥BC,AD=4,AB=AC=2 ,∠BAC=120°,若点P为△ABC内的动点满足直线DP与平面ABC所成角的正切值为2,则点P在△ABC内所成的轨迹的长度为
,∠BAC=120°,若点P为△ABC内的动点满足直线DP与平面ABC所成角的正切值为2,则点P在△ABC内所成的轨迹的长度为 
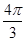 。
。
解析试题分析:因为∠BAD=90°,所以AD⊥AB,又AD⊥BC,且AB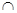 BC=B,所以AD⊥平面ABC。
BC=B,所以AD⊥平面ABC。
在平面ABC内,取点P,连PA,则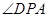 是DP与平面ABC所成角。
是DP与平面ABC所成角。
又因为AD=4,所以直线DP与平面ABC所成角的正切值为2,须AP=2,即点P在△ABC内所成的轨迹是以A为圆心,半径为2 的圆的一部分。
而∠BAC=120°=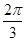 ,故点P在△ABC内所成的轨迹的长度为
,故点P在△ABC内所成的轨迹的长度为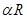 =
=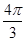 。
。
考点:本题主要考查立体几何中的垂直关系,角的计算,圆的定义,扇形弧长公式。
点评:典型题,综合性较强,考查知识全面,可谓之是“证算并重题”,较好地考查了数形结合思想及学生的逻辑推理能力、计算能力。解答本题的关键是认识到“点P在△ABC内所成的轨迹是以A为圆心,半径为2 的圆的一部分。”


科目:高中数学 来源: 题型:填空题
正三棱锥P—ABC中,CM=2PM,CN=2NB,对于以下结论:
①二面角B—PA—C大小的取值范围是( ,π);
,π);
②若MN⊥AM,则PC与平面PAB所成角的大小为 ;
;
③过点M与异面直线PA和BC都成 的直线有3条;
的直线有3条;
④若二面角B—PA—C大小为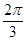 ,则过点N与平面PAC和平面PAB都成
,则过点N与平面PAC和平面PAB都成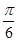 的直线有3条.
的直线有3条.
正确的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知一颗粒子等可能地落入如图所示的四边形ABCD内的任意位置,如果通过大量的实验发现粒子落入△BCD内的频率稳定在 附近,那么点A和点C到直线BD的距离之比约为
附近,那么点A和点C到直线BD的距离之比约为 
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知平行六面体ABCD-A1B1C1D1中,∠A1AD=∠A1AB=∠BAD=60°,AA1=AB=AD=1,E为A1D1的中点。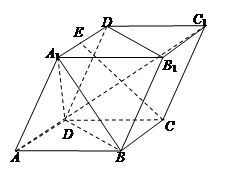
给出下列四个命题:①∠BCC1为异面直线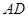 与CC1所成的角;②三棱锥A1-ABD是正三棱锥;③CE⊥平面BB1D1D;④
与CC1所成的角;②三棱锥A1-ABD是正三棱锥;③CE⊥平面BB1D1D;④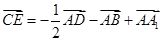 ;⑤|
;⑤|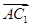 |=
|= .其中正确的命题有_____________.(写出所有正确命题的序号)
.其中正确的命题有_____________.(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
将一幅斜边长相等的直角三角板拼接成如图所示的空间图形,其中AD=BD=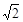 ,∠BAC=30°,若它们的斜边AB重合,让三角板ABD以AB为轴转动,则下列说法正确的是 .
,∠BAC=30°,若它们的斜边AB重合,让三角板ABD以AB为轴转动,则下列说法正确的是 .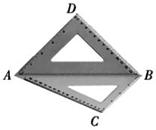
①当平面ABD⊥平面ABC时,C、D两点间的距离为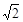 ;
;
②在三角板ABD转动过程中,总有AB⊥CD;
③在三角板ABD转动过程中,三棱锥D-ABC体积的最大值为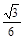 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com