
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() ,
,![]() 的值;
的值;
(2)若函数![]() 在
在![]() 和
和![]() 两处取得极值,求实数
两处取得极值,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由题意得:![]() ,
,![]() ,解得
,解得![]() ,
,![]() .
.
(2)由题意知:![]() 有两个零点
有两个零点![]() ,
,![]() ,
,
令![]() ,而
,而![]() .
.
对![]() 时和
时和![]() 时分类讨论,解得:
时分类讨论,解得:![]() .经检验,合题;
.经检验,合题;
(3)由题意得,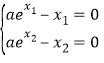 ,即
,即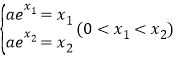 .
.
所以![]() ,令
,令![]() ,即
,即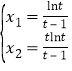 ,
,
令![]() ,求导,得
,求导,得![]() 在
在![]() 上单调递减,即
上单调递减,即![]() .
.
![]() ,
,![]() .令
.令![]() ,求导得
,求导得![]() 在
在![]() 上单调递减,得
上单调递减,得![]() 的取值范围.
的取值范围.
(1)![]() ,
,
由题意得:![]() ,即
,即![]() ,
,
![]() 即
即![]() ,所以
,所以![]() ,
,![]() .
.
(2)由题意知:![]() 有两个零点
有两个零点![]() ,
,![]() ,
,
令![]() ,而
,而![]() .
.
①当![]() 时,
时,![]() 恒成立
恒成立
所以![]() 单调递减,此时
单调递减,此时![]() 至多1个零点(舍).
至多1个零点(舍).
②当![]() 时,令
时,令![]() ,解得:
,解得:![]() ,
,
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() ,
,
因为![]() 有两个零点,所以
有两个零点,所以![]() ,
,
解得:![]() .
.
因为![]() ,
,![]() ,且
,且![]() ,
,
而![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() 在
在![]() 上有1个零点;
上有1个零点;
又因为![]() (易证
(易证![]() ),
),
则![]() 且
且![]() ,
,
而![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() 在
在![]() 上有1个零点.
上有1个零点.
综上:![]() .
.
(3)由题意得,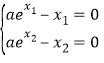 ,即
,即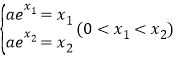 .
.
所以![]() ,令
,令![]() ,即
,即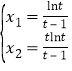 ,
,
令![]() ,
,![]() ,
,
令![]() ,而
,而![]() ,
,
所以![]() 在
在![]() 上单调递减,即
上单调递减,即![]() ,
,
所以![]() 在
在![]() 上单调递减,即
上单调递减,即![]() .
.
因为![]() ,
,![]() .
.
令![]() ,而
,而![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上单调递减,又
上单调递减,又![]() ,
,
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】已知点![]() 是抛物线
是抛物线![]() 的对称轴与准线的交点,点
的对称轴与准线的交点,点![]() 为抛物线的焦点,
为抛物线的焦点,![]() 在抛物线上且满足
在抛物线上且满足![]() ,当
,当![]() 取最大值时,点
取最大值时,点![]() 恰好在以
恰好在以![]() ,
,![]() 为焦点的双曲线上,则双曲线的离心率为( )
为焦点的双曲线上,则双曲线的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)满足:对于s,t∈[0,+∞),都有f(s)≥0,f(t)≥0,且f(s)+f(t)≤f(s+t),则称函数f (x)为“T函数”.
(I)试判断函数f1(x)=x2与f2(x)=lg(x+1)是否是“T函数”,并说明理由;
(Ⅱ)设f (x)为“T函数”,且存在x0∈[0,+∞),使f(f(x0))=x0.求证:f (x0) =x0;
(Ⅲ)试写出一个“T函数”f(x),满足f(1)=1,且使集合{y|y=f(x),0≤x≤1)中元素的个数最少.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1: ![]() (t为参数,t≠0),其中0≤α<π.在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sin θ,C3:ρ=2
(t为参数,t≠0),其中0≤α<π.在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sin θ,C3:ρ=2![]() cos θ.
cos θ.
(1)求C2与C3交点的直角坐标;
(2)若C1与C2相交于点A,C1与C3相交于点B,求|AB|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“人机大战,柯洁哭了,机器赢了”,2017年5月27日,![]() 岁的世界围棋第一人柯洁
岁的世界围棋第一人柯洁![]() 不敌人工智能系统AlphaGo,落泪离席.许多人认为这场比赛是人类的胜利,也有许多人持反对意见,有网友为此进行了调查.在参与调查的
不敌人工智能系统AlphaGo,落泪离席.许多人认为这场比赛是人类的胜利,也有许多人持反对意见,有网友为此进行了调查.在参与调查的![]() 男性中,有
男性中,有![]() 人持反对意见,
人持反对意见,![]() 名女性中,有
名女性中,有![]() 人持反对意见.再运用这些数据说明“性别”对判断“人机大战是人类的胜利”是否有关系时,应采用的统计方法是( )
人持反对意见.再运用这些数据说明“性别”对判断“人机大战是人类的胜利”是否有关系时,应采用的统计方法是( )
A.分层抽样B.回归分析C.独立性检验D.频率分布直方图
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次体育兴趣小组的聚会中,要安排6人的座位,使他们在如图所示的6个椅子中就坐,且相邻座位(如1与2,2与3)上的人要有共同的体育兴趣爱好.现已知这6人的体育兴趣爱好如下表所示,且小林坐在1号位置上,则4号位置上坐的是
小林 | 小方 | 小马 | 小张 | 小李 | 小周 | |
体育兴趣爱好 | 篮球,网球,羽毛球 | 足球,排球,跆拳道 | 篮球,棒球,乒乓球 | 击剑,网球,足球 | 棒球,排球,羽毛球 | 跆拳道,击剑,自行车 |

A.小方B.小张C.小周D.小马
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com