
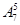 =2520(种).
=2520(种).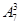 种方法,余下4人排在后排,有
种方法,余下4人排在后排,有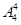 种方法,故共有
种方法,故共有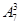 ·
·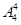 =5040(种).事实上,本小题即为7人排成一排的全排列,无任何限制条件.
=5040(种).事实上,本小题即为7人排成一排的全排列,无任何限制条件.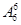 种方法,故共有5×
种方法,故共有5×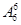 =3600(种).
=3600(种).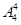 种方法,再将4名女生进行全排列,也有
种方法,再将4名女生进行全排列,也有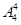 种方法,故共有
种方法,故共有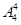 ×
×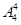 =576(种).
=576(种).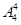 种方法,再在女生之间及首尾空出的5个空位中任选3个空位排男生,有
种方法,再在女生之间及首尾空出的5个空位中任选3个空位排男生,有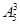 种方法,故共有
种方法,故共有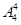 ×
×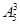 =1440(种).
=1440(种). 种方法,再从剩下的5人中选3人排到中间,有
种方法,再从剩下的5人中选3人排到中间,有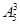 种方法,最后把甲、乙及中间3人看作一个整体,与剩余2人排列,有
种方法,最后把甲、乙及中间3人看作一个整体,与剩余2人排列,有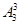 种方法,故共有
种方法,故共有 ×
×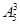 ×
×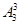 =720(种).
=720(种).

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.60种 | B.70种 | C.75种 | D.150种 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 放方案有
放方案有查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com