
【题目】某县畜牧技术员张三和李四9年来一直对该县山羊养殖业的规模进行跟踪调查,张三提供了该县某山羊养殖场年养殖数量y(单位:万只)与相成年份x(序号)的数据表和散点图(如图所示),根据散点图,发现y与x有较强的线性相关关系,李四提供了该县山羊养殖场的个数z(单位:个)关于x的回归方程![]() .
.

(1)根据表中的数据和所给统计量,求y关于x的线性回归方程(参考统计量:![]() );
);
(2)试估计:①该县第一年养殖山羊多少万只?
②到第几年,该县山羊养殖的数量与第一年相比缩小了?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某桶装水经营部每天的房租、人员工资等固定成本为300元,每桶水的进价是8元,销售单价与日均销售量的关系如表所示:
销售单价/元 | 9 | 10 | 11 | 12 | 13 | 14 |
日均销售量/桶 | 550 | 500 | 450 | 400 | 350 | 300 |
请根据以上数据分析,这个店怎样定每桶水的单价才能获得最大利润?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子![]() 和
和![]() 中均装有若干个大小相同的红球和白球,从
中均装有若干个大小相同的红球和白球,从![]() 中摸出一个红球的概率是
中摸出一个红球的概率是![]() ,从
,从![]() 中摸出一个红球的概率为
中摸出一个红球的概率为![]() .
.
(1)从![]() 中有放回地摸球,每次摸出1个,有3次摸到红球即停止,求恰好摸5次停止的概率.
中有放回地摸球,每次摸出1个,有3次摸到红球即停止,求恰好摸5次停止的概率.
(2)若![]() 、
、![]() 两个袋子中的球数之比为
两个袋子中的球数之比为![]() ,将
,将![]() 、
、![]() 中的球装在一起后,从中摸出一个红球的概率是
中的球装在一起后,从中摸出一个红球的概率是![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,以原点为极点,以![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(I)若曲线![]() ,参数方程为:
,参数方程为:![]() (
(![]() 为参数),求曲线
为参数),求曲线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程
的普通方程
(Ⅱ)若曲线![]() ,参数方程为
,参数方程为![]() (
(![]() 为参数),
为参数),![]() ,且曲线
,且曲线![]() ,与曲线
,与曲线![]() 交点分别为
交点分别为![]() ,求
,求![]() 的取值范围,
的取值范围,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,将圆
中,将圆![]() 上每一点的横坐标保持不变,纵坐标变为原来的
上每一点的横坐标保持不变,纵坐标变为原来的![]() 倍,再把所得曲线上每一点向下平移1个单位得到曲线
倍,再把所得曲线上每一点向下平移1个单位得到曲线![]() .以
.以![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出![]() 的参数方程和
的参数方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,求使
上,求使![]() 取最小值时点
取最小值时点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新个税法于2019年1月1日进行实施.为了调查国企员工对新个税法的满意程度,研究人员在![]() 地各个国企中随机抽取了1000名员工进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中
地各个国企中随机抽取了1000名员工进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中![]() .
.
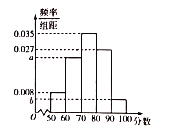
(1)求![]() 的值并估计被调查的员工的满意程度的中位数;(计算结果保留两位小数)
的值并估计被调查的员工的满意程度的中位数;(计算结果保留两位小数)
(2)若按照分层抽样从![]() ,
,![]() 中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在
中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com