
【题目】(I)已知函数f(x)=rx﹣xr+(1﹣r)(x>0),其中r为有理数,且0<r<1.求f(x)的最小值;
(II)试用(I)的结果证明如下命题:设a1≥0,a2≥0,b1 , b2为正有理数,若b1+b2=1,则a1b1a2b2≤a1b1+a2b2;
(III)请将(II)中的命题推广到一般形式,并用数学归纳法证明你所推广的命题.注:当α为正有理数时,有求导公式(xα)r=αxα﹣1 .
【答案】(I)解:求导函数可得:f′(x)=r(1﹣xr﹣1),令f′(x)=0,解得x=1;
当0<x<1时,f′(x)<0,所以f(x)在(0,1)上是减函数;
当x>1时,f′(x)>0,所以f(x)在(0,1)上是增函数
所以f(x)在x=1处取得最小值f(1)=0;
(II)解:由(I)知,x∈(0,+∞)时,有f(x)≥f(1)=0,即xr≤rx+(1﹣r)①
若a1 , a2中有一个为0,则a1b1a2b2≤a1b1+a2b2成立;
若a1 , a2均不为0,∵b1+b2=1,∴b2=1﹣b1 ,
∴①中令 ![]() ,可得a1b1a2b2≤a1b1+a2b2成立
,可得a1b1a2b2≤a1b1+a2b2成立
综上,对a1≥0,a2≥0,b1 , b2为正有理数,若b1+b2=1,则a1b1a2b2≤a1b1+a2b2;②
(III)解:(II)中的命题推广到一般形式为:设a1≥0,a2≥0,…,an≥0,b1 , b2 , …,bn为正有理数,若b1+b2+…+bn=1,则a1b1a2b2…anbn≤a1b1+a2b2+…anbn;③
用数学归纳法证明
(1)当n=1时,b1=1,a1≤a1 , ③成立
(2)假设当n=k时,③成立,即a1≥0,a2≥0,…,ak≥0,b1 , b2 , …,bk为正有理数,若b1+b2+…+bk=1,则a1b1a2b2…akbk≤a1b1+a2b2+…akbk .
当n=k+1时,a1≥0,a2≥0,…,ak+1≥0,b1 , b2 , …,bk+1为正有理数,若b1+b2+…+bk+1=1,则1﹣bk+1>0
于是a1b1a2b2…akbkak+1bk+1=(a1b1a2b2…akbk)ak+1bk+1= ![]() ak+1bk+1
ak+1bk+1
∵ ![]() +
+ ![]() +…+
+…+ ![]() =1
=1
∴ ![]() ≤
≤ ![]() +
+ ![]() +…+
+…+ ![]()
= ![]()
∴ ![]() ak+1bk+1≤
ak+1bk+1≤ ![]() (1﹣bk+1)+ak+1bk+1 ,
(1﹣bk+1)+ak+1bk+1 ,
∴a1b1a2b2…akbkak+1bk+1≤a1b1+a2b2+…akbk+ak+1bk+1 .
∴当n=k+1时,③成立
由(1)(2)可知,对一切正整数,推广的命题成立.
【解析】(I)求导函数,令f′(x)=0,解得x=1;确定函数在(0,1)上是减函数;在(0,1)上是增函数,从而可求f(x)的最小值;(II)由(I)知,x∈(0,+∞)时,有f(x)≥f(1)=0,即xr≤rx+(1﹣r),分类讨论:若a1 , a2中有一个为0,则a1b1a2b2≤a1b1+a2b2成立;若a1 , a2均不为0, ![]() ,可得a1b1a2b2≤a1b1+a2b2成立(III)(II)中的命题推广到一般形式为:设a1≥0,a2≥0,…,an≥0,b1 , b2 , …,bn为正有理数,若b1+b2+…+bn=1,则a1b1a2b2…anbn≤a1b1+a2b2+…anbn;
,可得a1b1a2b2≤a1b1+a2b2成立(III)(II)中的命题推广到一般形式为:设a1≥0,a2≥0,…,an≥0,b1 , b2 , …,bn为正有理数,若b1+b2+…+bn=1,则a1b1a2b2…anbn≤a1b1+a2b2+…anbn;
用数学归纳法证明:(1)当n=1时,b1=1,a1≤a1 , 推广命题成立;(2)假设当n=k时,推广命题成立,证明当n=k+1时,利用a1b1a2b2…akbkak+1bk+1=(a1b1a2b2…akbk)ak+1bk+1= ![]() ak+1bk+1 , 结合归纳假设,即可得到结论.
ak+1bk+1 , 结合归纳假设,即可得到结论.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD-A1B1C1D1中,AB=3,AD=2,AA1=1,以长方体的八个顶点中的两点为起点和终点的向量中.

(1)单位向量共有多少个?
(2)试写出模为![]() 的所有向量.
的所有向量.
(3)试写出与![]() 相等的所有向量.
相等的所有向量.
(4)试写出![]() 的相反向量.
的相反向量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且a,b,c成等比数列,sinB= ![]() ,
,
(1)求 ![]() +
+ ![]() 的值;
的值;
(2)若 ![]()
![]() =12,求a+c的值.
=12,求a+c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,双曲线 ![]() =1(a,b>0)的两顶点为A1 , A2 , 虚轴两端点为B1 , B2 , 两焦点为F1 , F2 . 若以A1A2为直径的圆内切于菱形F1B1F2B2 , 切点分别为A,B,C,D.则: (Ⅰ)双曲线的离心率e=;
=1(a,b>0)的两顶点为A1 , A2 , 虚轴两端点为B1 , B2 , 两焦点为F1 , F2 . 若以A1A2为直径的圆内切于菱形F1B1F2B2 , 切点分别为A,B,C,D.则: (Ⅰ)双曲线的离心率e=;
(Ⅱ)菱形F1B1F2B2的面积S1与矩形ABCD的面积S2的比值 ![]() = .
= . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且asin B=-bsin![]() .
.
(1)求A;
(2)若△ABC的面积S=![]() c2,求sin C的值.
c2,求sin C的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=AC=3,AB=![]() ,BE=
,BE=![]() EC,AD=2DC.
EC,AD=2DC.

(1)证明:DE⊥平面PAE;
(2)求二面角A-PE-B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知CD是等边三角形ABC的AB边上的高,E,F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.
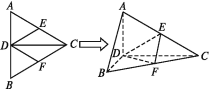
(1)求直线BC与平面DEF所成角的余弦值;
(2)在线段BC上是否存在一点P,使AP⊥DE?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个几何体三视图的正视图和侧视图为边长为2锐角60°的菱形,俯视图为正方形,则此几何体的内切球表面积为( ) 
A.8π
B.4π
C.3π
D.2π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,底面△ABC是直角三角形,AB=AC=1,点P是棱BB1上一点,满足 ![]() (0≤λ≤1).
(0≤λ≤1). 
(1)若λ= ![]() ,求直线PC与平面A1BC所成角的正弦值;
,求直线PC与平面A1BC所成角的正弦值;
(2)若二面角P﹣A1C﹣B的正弦值为 ![]() ,求λ的值.
,求λ的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com