
【题目】在如图所示的五面体![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,四边形
,四边形![]() 为正方形,平面
为正方形,平面![]() 平面
平面![]() .
.
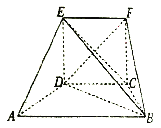
(1)证明:在线段![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 平面
平面![]() ;
;
(2)求![]() 的长.
的长.
【答案】(1)证明见解析;(2)2.
【解析】试题分析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,由正方形的性质可证明四边形
,由正方形的性质可证明四边形![]() 为平行四边形,故
为平行四边形,故![]() ,由线面平行的判定定理可得
,由线面平行的判定定理可得![]() 平面
平面![]() ,点
,点![]() 就是符合条件的点;(2)由平面
就是符合条件的点;(2)由平面![]() 平面
平面![]() 及可得
及可得![]() 平面
平面![]() ,可得
,可得![]() ,在
,在![]() 中,由余弦定理,得
中,由余弦定理,得![]() ,由(1)得
,由(1)得![]() ,根据勾股定理可得
,根据勾股定理可得![]() .
.
试题解析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ;
;
因为![]() ,
, ![]() ,
,
![]() ,所以
,所以![]() ,又四边形
,又四边形![]() 是正方形,所以
是正方形,所以![]() ,
, ![]() ,
,
故四边形![]() 为平行四边形,故
为平行四边形,故![]() ,
,
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)因为平面![]() 平面
平面![]() ,四边形
,四边形![]() 为正方形,所以
为正方形,所以![]() ,
,
所以![]() 平面
平面![]() .
.
在![]() 中,因为
中,因为![]() ,故
,故![]() ,又
,又![]() ,
,
所以由余弦定理,得![]() ,由(1)得
,由(1)得![]()
故![]() .
.

【方法点晴】本题主要考查线面平行的判定定理、面面垂直的性质定理,属于难题. 证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
【题目】某校为了鼓励学生热心公益,服务社会,成立了“慈善义工社”.2017年12月,该校“慈善义工社”为学生提供了4次参加公益活动的机会,学生可通过网路平台报名参加活动.为了解学生实际参加这4次活动的情况,该校随机抽取100名学生进行调查,数据统计如下表,其中“√”表示参加,“×”表示未参加.

(Ⅰ)从该校所有学生中任取一人,试估计其2017年12月恰参加了2次学校组织的公益活动的概率;
(Ⅱ)若在已抽取的100名学生中,2017年12月恰参加了1次活动的学生比4次活动均未参加的学生多17人,求![]() 的值;
的值;
(Ⅲ)若学生参加每次公益活动可获得10个公益积分,试估计该校4000名学生中,2017年12月获得的公益积分不少于30分的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,(其中
,(其中![]() ,
, ![]() 为自然对数的底数,
为自然对数的底数, ![]() ……).
……).
(1)令![]() ,若
,若![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的值;
的值;
(2)在(1)的条件下,设![]() 为整数,且对于任意正整数
为整数,且对于任意正整数![]() ,
, ![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.

(1)证明:EM⊥BF;
(2)求平面BEF与平面ABC所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,上顶点为
,上顶点为![]() ,直线
,直线![]() 与直线
与直线![]() 垂直,椭圆
垂直,椭圆![]() 经过点
经过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 作椭圆
作椭圆![]() 的两条互相垂直的弦
的两条互相垂直的弦![]() .若弦
.若弦![]() 的中点分别为
的中点分别为![]() ,证明:直线
,证明:直线![]() 恒过定点.
恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于集合![]() ,定义了一种运算“
,定义了一种运算“![]() ”,使得集合
”,使得集合![]() 中的元素间满足条件:如果存在元素
中的元素间满足条件:如果存在元素![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ,则称元素
,则称元素![]() 是集合
是集合![]() 对运算“
对运算“![]() ”的单位元素.例如:
”的单位元素.例如: ![]() ,运算“
,运算“![]() ”为普通乘法;存在
”为普通乘法;存在![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ,所以元素
,所以元素![]() 是集合
是集合![]() 对普通乘法的单位元素.
对普通乘法的单位元素.
下面给出三个集合及相应的运算“![]() ”:
”:
①![]() ,运算“
,运算“![]() ”为普通减法;
”为普通减法;
②![]() {
{![]() 表示
表示![]() 阶矩阵,
阶矩阵, ![]() },运算“
},运算“![]() ”为矩阵加法;
”为矩阵加法;
③![]() (其中
(其中![]() 是任意非空集合),运算“
是任意非空集合),运算“![]() ”为求两个集合的交集.
”为求两个集合的交集.
其中对运算“![]() ”有单位元素的集合序号为( )
”有单位元素的集合序号为( )
A. ①②; B. ①③; C. ①②③; D. ②③.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 为圆柱
为圆柱![]() 的母线,
的母线, ![]() 是底面圆
是底面圆![]() 的直径,
的直径, ![]() 是
是![]() 的中点.
的中点.
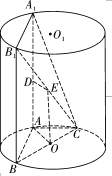
(Ⅰ)问: ![]() 上是否存在点
上是否存在点![]() 使得
使得![]() 平面
平面![]() ?请说明理由;
?请说明理由;
(Ⅱ)在(Ⅰ)的条件下,若![]() 平面
平面![]() ,假设这个圆柱是一个大容器,有条体积可以忽略不计的小鱼能在容器的任意地方游弋,如果小鱼游到四棱锥
,假设这个圆柱是一个大容器,有条体积可以忽略不计的小鱼能在容器的任意地方游弋,如果小鱼游到四棱锥![]() 外会有被捕的危险,求小鱼被捕的概率.
外会有被捕的危险,求小鱼被捕的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 经过
经过![]() 为坐标原点,线段
为坐标原点,线段![]() 的中点在圆
的中点在圆![]() 上.
上.
(1)求![]() 的方程;
的方程;
(2)直线![]() 不过曲线
不过曲线![]() 的右焦点
的右焦点![]() ,与
,与![]() 交于
交于![]() 两点,且
两点,且![]() 与圆
与圆![]() 相切,切点在第一象限,
相切,切点在第一象限, ![]() 的周长是否为定值?并说明理由.
的周长是否为定值?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com