
分析 (Ⅰ)求出函数f(x)的导数,解关于导函数的方程,求出函数的单调区间和极值即可;
(Ⅱ)求出函数f(x)的最小值,通过讨论a的范围,判断g(x)的单调性,从而确定a的范围即可.
解答 解:(Ⅰ)∵f(x)的定义域是(0,1)∪(1,+∞),
∴$f'(x)=\frac{{2xlnkx-{x^2}•\frac{1}{x}}}{{2{{ln}^2}kx}}=\frac{{x({2lnkx-1})}}{{2{{ln}^2}kx}}$.
由已知$f'({\sqrt{e}})=0$得k=1,
∴$f(x)=\frac{x^2}{2lnx}$
从而f'(x)、f(x)随x的变化如下表
| x | (0,1) | $({1\;,\;\sqrt{e}})$ | $\sqrt{e}$ | $({\sqrt{e}\;,\;+∞})$ |
| f'(x) | - | - | 0 | + |
| f(x) | ↘ | ↘ | 极小 | ↗ |
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
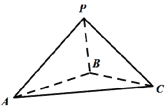 如图所示,四面体P-ABC中,$∠APB=∠BPC=∠CPA=\frac{π}{2}$,PA=4,PB=2,$PC=\sqrt{5}$,则四面体P-ABC的外接球的表面积为25π.
如图所示,四面体P-ABC中,$∠APB=∠BPC=∠CPA=\frac{π}{2}$,PA=4,PB=2,$PC=\sqrt{5}$,则四面体P-ABC的外接球的表面积为25π.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
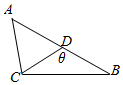 △ABC中,角A,B,C的对边分别为a,b,c,已知$\frac{{\sqrt{3}sinC}}{cosB}=\frac{c}{b}$.
△ABC中,角A,B,C的对边分别为a,b,c,已知$\frac{{\sqrt{3}sinC}}{cosB}=\frac{c}{b}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 井号I | 1 | 2 | 3 | 4 | 5 | 6 |
| 坐标(x,y)(km) | (2,30) | (4,40) | (5,60) | (6,50) | (8,70) | (1,y) |
| 钻探深度(km) | 2 | 4 | 5 | 6 | 8 | 10 |
| 出油量(L) | 40 | 70 | 110 | 90 | 160 | 205 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com