
 如图,ABCD-A1B1C1D1是正方体,O、M、N分别是B1D1、AB1、AD1的中点,直线A1C交平面AB1D1于点P.
如图,ABCD-A1B1C1D1是正方体,O、M、N分别是B1D1、AB1、AD1的中点,直线A1C交平面AB1D1于点P.分析 (Ⅰ)证明:MN∥B1D1,即可证明MN∥平面CB1D1;
(Ⅱ)①证明AA1与CC1共面,再证明P、O、∈平面AA1C1C,即可证明A、P、O、C四点共面;
②P是平面AA1C1C与平面AB1D1的公共点,故根据公理3,P在交线AO上,即可证明A、P、O三点共线.
解答 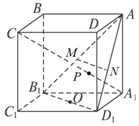 证明:(Ⅰ)∵M、N分别是AB1、AD1的中点,
证明:(Ⅰ)∵M、N分别是AB1、AD1的中点,
∴MN∥B1D1.(2分)
∵B1D1?平面CB1D1,MN?平面CB1D1,
∴MN∥平面CB1D1.(4分)
(Ⅱ)①∵ABCD-A1B1C1D1是正方体,∴AA1∥CC1,即AA1与CC1共面.(5分)
∵A1C1?平面AA1C1C,O∈A1C1,∴O∈平面AA1C1C.(6分)
∵A1C?平面AA1C1C,P∈A1C,∴P∈平面AA1C1C.(7分)
∴A、P、O、C∈平面AA1C1C,即A、P、O、C四点共面.(8分)
②∵AO是平面AA1C1C与平面AB1D1的交线,且P是平面AA1C1C与平面AB1D1的公共点,
故根据公理3,P在交线AO上.即A、P、O三点共线.(11分)
点评 本题考查线面平行的证明,考查平面的基本性质,考查学生分析解决问题的能力,属于中档题.


 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
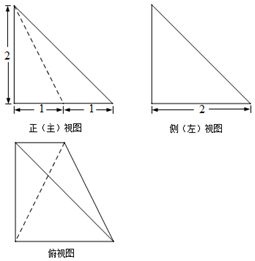
| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (1,2) | C. | ($\frac{1}{2}$,1) | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-$\sqrt{2}$ | B. | $\sqrt{2}$-1 | C. | 5-$\sqrt{2}$ | D. | $\sqrt{2}$-5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com