(本题满分l0分)
如图，已知抛物线M：x2=4py(p＞0)的准线为ι，N为ι上的一个动点，过点N作抛物线M的两条切线，切点分别为A，B，再分别过A，B两点作ι的垂线，垂足分别为C，D．
(1)求证：直线AB必经过y轴上的一个定点Q，并写出点Q的坐标；
(2)若△ACN，△BDN，△ANB的面积依次构成等差数列，求此时点N的坐标．
【必做题】
解法一：（1）因为抛物线的准线
的方程为
，
所以可设点
的坐标分别为
，
，
，则
，
，
由
，得
，求导数得
，于是
，
即
，化简得
，
同理可得
，
所以
和
是关于
的方程
两个实数根，所以
，
且
．
在直线
的方程
中，
令
，得
=
为定值，
所以直线必经过
轴上的一个定点
，即抛物线的焦点．……………………………5分
(2)由（1）知
，所以
为线段
的中点，取线段的中点
，
因为
是抛物线的焦点，所以
，所以
，
所以
，
又因为
，
，
所以
，
，
成等差数列，即
成等差数列，
即
成等差数列，所以
，
，
所以
，
，
时，
，
，
时，
，
，所以所求点
的坐标为
．………………………………………………………………10分
解法二：（1）因为已知抛物线的准线的方程为，所以可设点
的坐标分别为，，，则，，
设过点与抛物线相切的直线方程为
，与抛物线方程
联立，消去得
，
因为直线与抛物线相切，所以
，即
，解得
，此时两切点横坐标分别为
，
在直线的方程中，令得
=为定值，
所以直线必经过轴上的一个定点，即抛物线的焦点．……………………………5分
（2）由（1）知两切线的斜率分别为，则
，所以
，
连接
，则直线斜率为
，
又因为直线的斜率
，
所以
，
所以
，又因为，所以
，
所以
和
的面积成等差数列，所以成等差数列，
所以成等差数列，所以，，
所以，，
时，，，
时，，
，
所以所求点的坐标为
． …………………………………………………………10分
（以上各题如考生另有解法，请参照本评分标准给分）
阅读快车系列答案科目：高中数学 来源：2011届辽宁省东北育才学校高三第一次模拟考试数学理卷 题型：解答题
选修4—4:坐标系与参数方程
(本题满分l0分)
在直角坐标系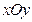
中，以O为极点，
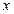轴正半轴为极轴建立极坐标系，直线
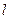的极坐标方程为
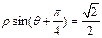．圆O的参数方程为
，（
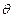为参数，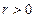
）
(I)求圆心的一个极坐标；
(Ⅱ)当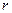
为何值时，圆O上的点到直线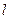的最大距离为3．
查看答案和解析>>
科目：高中数学 来源：2010-2011学年辽宁省高三第一次模拟考试数学理卷 题型：解答题
选修4—4:坐标系与参数方程
(本题满分l0分)
在直角坐标系
中，以O为极点，
轴正半轴为极轴建立极坐标系，直线
的极坐标方程为
．圆O的参数方程为
，（
为参数，
）
(I)求圆心的一个极坐标；
(Ⅱ)当
为何值时，圆O上的点到直线的最大距离为3．
查看答案和解析>>
科目：高中数学 来源： 题型：
(本题满分l0分)
某电视台综艺频道组织的闯关游戏，游戏规定前两关至少过一关才有资格闯第三关，闯关者闯第一关成功得3分，闯第二关成功得3分，闯第三关成功得4分．现有一位参加游戏者单独面第一关、第二关、第三关成功的概率分别为
，
，
，记该参加者闯三关所得总分为ζ．
(1)求该参加者有资格闯第三关的概率；
(2)求ζ的分布列和数学期望．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com