
【题目】设函数f(x)=|x+4|.
(1)若y=f(2x+a)+f(2x﹣a)最小值为4,求a的值;
(2)求不等式f(x)>1﹣ ![]() x的解集.
x的解集.
【答案】
(1)解:由题意,函数f(x)=|x+4|.
那么y=f(2x+a)+f(2x﹣a)=|2x+a+4|+|2x﹣a+4|≥|2x+a﹣4﹣(2x﹣a+4)|=|2a|
∵最小值为4,即|2a|=3,
∴a= ![]()
(2)解:函数f(x)=|x+4|= 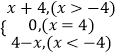
∴不等式f(x)>1﹣ ![]() x等价于
x等价于 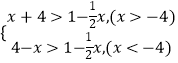 ,解得:x>﹣2或x<﹣4
,解得:x>﹣2或x<﹣4
故得不等式f(x)>1﹣ ![]() x的解集为{x|x>﹣2或x<﹣4}
x的解集为{x|x>﹣2或x<﹣4}
【解析】(1)求出y的解析式,利用绝对值不等式即可求解a的值.(2)函数含有绝对值,即可考虑到分类讨论去掉绝对值号,分别讨论当x=﹣4时,当x>﹣4时,当x<﹣4的情况,可得不同解析式求解不等式即可.
【考点精析】根据题目的已知条件,利用绝对值不等式的解法的相关知识可以得到问题的答案,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.


科目:高中数学 来源: 题型:
【题目】如图,在三棱锥V﹣ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=![]() ,O,M分别为AB,VA的中点.
,O,M分别为AB,VA的中点.
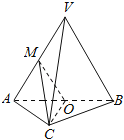
(1)求证:VB∥平面MOC;
(2)求证:平面MOC⊥平面VAB
(3)求三棱锥V﹣ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心在![]() 轴上的圆
轴上的圆![]() 与直线
与直线![]() 切于点
切于点![]() .圆
.圆![]() :
: ![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)已知![]() ,圆
,圆![]() 与
与![]() 轴相交于两点
轴相交于两点![]() (点
(点![]() 在点
在点![]() 的右侧).过点
的右侧).过点![]() 任作一条倾斜角不为0的直线与圆
任作一条倾斜角不为0的直线与圆![]() 相交于
相交于![]() 两点.问:是否存在实数
两点.问:是否存在实数![]() ,使得
,使得![]() ?若存在,求出实数
?若存在,求出实数![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的公差d≠0,且a3 , a5 , a15成等比数列,若a1=3,Sn为数列an的前n项和,则anSn的最小值为( )
A.0
B.﹣3
C.﹣20
D.9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知长方形ABCD中,AB=2AD,M为DC的中点,将△ADM沿AM折起,使得平面ADM⊥平面ABCM. 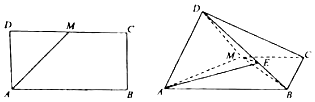
(1)求证:AD⊥BM;
(2)若 ![]() =2
=2 ![]() ,求二面角E﹣AM﹣D的正弦值.
,求二面角E﹣AM﹣D的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为(-2,2),函数g(x)=f(x-1)+f(3-2x).
(1)求函数g(x)的定义域;
(2)若f(x)是奇函数,且在定义域上单调递减,求不等式g(x)≤0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年6月22日“国际教育信息化大会”在山东青岛开幕.为了解哪些人更关注“国际教育信息化大会”,某机构随机抽取了年龄在15—75岁之间的100人进行调查,并按年龄绘制成频率分布直方图,如图所示,其分组区间为: ![]() .把年龄落在区间自
.把年龄落在区间自![]() 和
和![]() 内的人分别称为“青少年”和“中老年”.
内的人分别称为“青少年”和“中老年”.

关注 | 不关注 | 合计 | |
青少年 | 15 | ||
中老年 | |||
合计 | 50 | 50 | 100 |
(1)根据频率分布直方图求样本的中位数(保留两位小数)和众数;
(2)根据已知条件完成下面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为“中老年”比“青少年”更加关注“国际教育信息化大会”;
的把握认为“中老年”比“青少年”更加关注“国际教育信息化大会”;
临界值表:
附:参考公式
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
 ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com