
(09年聊城期末理)(12分)
如图,矩形ABCD,![]() 平面ABE,AE=EB=BC=2,F为CE是的点,且
平面ABE,AE=EB=BC=2,F为CE是的点,且![]() 平面ACE。
平面ACE。
(1)求证:![]() 平面BCE;
平面BCE;
(2)求二面角B―AC―E的大小。
|
解析:(1)证明:![]() 平面ABE,AD//BC。
平面ABE,AD//BC。
![]() 平面ABE,则
平面ABE,则![]() …………2分
…………2分
又![]() 平面ACE,则
平面ACE,则![]()
![]() 平面BCE。…………5分
平面BCE。…………5分
|
(2)方法一:取AB的中点H,CD的中点N,则HN//AD
![]() 平面ABE,
平面ABE,![]() 平面ABE,
平面ABE,
![]()
以HE所在直线为![]() 轴,HB所在直线为
轴,HB所在直线为![]() 轴,
轴,
HN所在直线为z轴,
建立空间直角坐标系,
则,![]()
![]()
平面BAC的一个法向量![]() …………8分
…………8分
设平面EAC的一个法向量![]() ,
,
由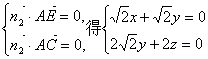
所以
令![]() …………10分
…………10分

![]()
![]() 二面角B―AC―E的大小为60°…………12分
二面角B―AC―E的大小为60°…………12分
方法二:过E作![]()
![]() 平面ABE,DA
平面ABE,DA![]() 平面ABCD,
平面ABCD,
![]() 平面ABCD
平面ABCD![]() 平面ABE,
平面ABE,
![]() 平面ABCD。
平面ABCD。
|
![]() 平面EHM。
平面EHM。
![]() 是
是
二面角B―AC―E的平面角。…………8分
在![]()
![]()
![]() ∽
∽![]()
![]()
又![]()
![]()
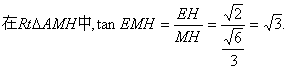
![]()
故二面角B―AC―E的大小为60°…………12分


科目:高中数学 来源: 题型:
(09年聊城期末理)(12分)
已知圆![]() (点O为坐标原点),一条直线
(点O为坐标原点),一条直线![]() 与圆O相切,并与椭圆
与圆O相切,并与椭圆![]() 交于不 同的两点A、B。
交于不 同的两点A、B。
(1)设![]() 的表达式;
的表达式;
(2)若![]() ,求三角形OAB的面积。
,求三角形OAB的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com