
【题目】如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1 , 焦点为F2;以F1 , F2为焦点,离心率e=![]() 的椭圆C2与抛物线C1在x轴上方的交点为P,延长PF2交抛物线于点Q,M是抛物线C1上一动点,且M在P与Q之间运动.
的椭圆C2与抛物线C1在x轴上方的交点为P,延长PF2交抛物线于点Q,M是抛物线C1上一动点,且M在P与Q之间运动.
当m=1时,求椭圆C2的方程;
科目:高中数学 来源: 题型:
【题目】已知数列{an}(n=1,2,3,4,5)满足a1=a5=0,且当2≤k≤5时,(ak﹣ak﹣1)2=1,令S=![]() , 则S不可能的值是( )
, 则S不可能的值是( )
A.4
B.0
C.1
D.-4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}前n项和Sn满足Sn+1=a2Sn+a1 , 其中a2≠0.
(Ⅰ)求证数列{an}是首项为1的等比数列;
(Ⅱ)当a2=2时,是否存在等差数列{bn},使得a1bn+a2bn﹣1+a3bn﹣2+…+anb1=2n+1﹣n﹣2对一切n∈N*都成立?若存在,求出bn;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
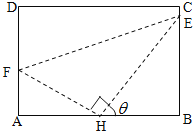
【题目】如图,某污水处理厂要在一个矩形污水处理池![]() 的池底水平铺设污水净化管道(
的池底水平铺设污水净化管道(![]() ,
,![]() 是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口
是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口![]() 是
是![]() 的中点,
的中点,![]() 分别落在线段
分别落在线段![]() 上.已知
上.已知![]() 米,
米,![]() 米,记
米,记![]() .
.
(1)试将污水净化管道的长度![]() 表示为
表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)若![]() ,求此时管道的长度
,求此时管道的长度![]() ;
;
(3)当![]() 取何值时,污水净化效果最好?并求出此时管道的长度.
取何值时,污水净化效果最好?并求出此时管道的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在区间[a,b]上的连续函数y=f(x),如果![]() ,使得
,使得![]() ,则称
,则称![]() 为区间[a,b]上的“中值点”,下列函数:
为区间[a,b]上的“中值点”,下列函数:
①![]() ; ②
; ②![]() ; ③
; ③![]() ; ④
; ④![]() 中,在区间[O,1]上“中值点”多于一个的函数序号为( )
中,在区间[O,1]上“中值点”多于一个的函数序号为( )
A. ①② B. ①③ C. ②③ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为调查高三年学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图(1))和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在170~175cm的男生人数有16人.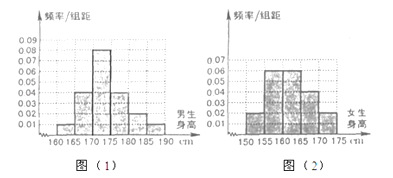
(Ⅰ)试问在抽取的学生中,男、女生各有多少人?
(Ⅱ)根据频率分布直方图,完成下列的2×2列联表,并判断能有多大(百分几)的把握认为“身高与性别有关”?
≥170cm | <170cm | 总计 | |
男生身高 | |||
女生身高 | |||
总计 |
(Ⅲ)在上述80名学生中,从身高在170~175cm之间的学生中按男、女性别分层抽样的方法,抽出5人,从这5人中选派3人当旗手,求3人中恰好有一名女生的概率.
参考公式:K2=![]()
参考数据:
P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com