
【题目】如图,已知点P在圆柱OO1的底面⊙O上,![]() 分别为⊙O、⊙O1的直径,且
分别为⊙O、⊙O1的直径,且![]() 平面
平面![]() .
.
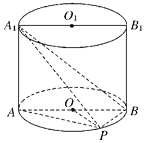
(1)求证:![]() ;
;
(2)若圆柱![]() 的体积
的体积![]() ,
,
①求三棱锥A1﹣APB的体积.
②在线段AP上是否存在一点M,使异面直线OM与![]() 所成角的余弦值为
所成角的余弦值为![]() ?若存在,请指出M的位置,并证明;若不存在,请说明理由.
?若存在,请指出M的位置,并证明;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】函数![]() (其中
(其中![]() ,
,![]() ,
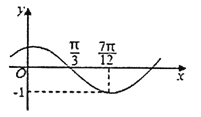
,![]() )的图象如图所示,为了得到
)的图象如图所示,为了得到![]() 的图象,只需把
的图象,只需把![]() 的图象上所有的点()
的图象上所有的点()
A. 向右平移![]() 个单位长度B. 向左平移
个单位长度B. 向左平移![]() 个单位长度
个单位长度
C. 向右平移![]() 个单位长度D. 向左平移
个单位长度D. 向左平移![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电影院共有![]() 个座位,某天,这家电影院上、下午各演一场电影.看电影的是甲、乙、丙三所中学的学生,三所学校的观影人数分别是985人,1010人,2019人(同一所学校的学生既可看上午场,又可看下午场,但每人只能看一场).已知无论如何排座位,这天观影时总存在这样的一个座位,上、下午在这个座位上坐的是同一所学校的学生,那么
个座位,某天,这家电影院上、下午各演一场电影.看电影的是甲、乙、丙三所中学的学生,三所学校的观影人数分别是985人,1010人,2019人(同一所学校的学生既可看上午场,又可看下午场,但每人只能看一场).已知无论如何排座位,这天观影时总存在这样的一个座位,上、下午在这个座位上坐的是同一所学校的学生,那么![]() 的可能取值有__________个.
的可能取值有__________个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是()
A. 锐角是第一象限的角,所以第一象限的角都是锐角;
B. 如果向量![]() ,则
,则![]() ;
;
C. 在![]() 中,记
中,记![]() ,
,![]() ,则向量
,则向量![]() 与
与![]() 可以作为平面ABC内的一组基底;
可以作为平面ABC内的一组基底;
D. 若![]() ,
,![]() 都是单位向量,则
都是单位向量,则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
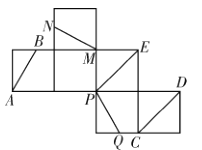
【题目】如图是一正方体的表面展开图.![]() 、
、![]() 、
、![]() 都是所在棱的中点.则在原正方体中:①
都是所在棱的中点.则在原正方体中:①![]() 与
与![]() 异面;②
异面;②![]() 平面
平面![]() ;③平面
;③平面![]() 平面
平面![]() ;④
;④![]() 与平面
与平面![]() 形成的线面角的正弦值是
形成的线面角的正弦值是![]() ;⑤二面角
;⑤二面角![]() 的余弦值为
的余弦值为![]() .其中真命题的序号是______.
.其中真命题的序号是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com