
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
分析 可画出图形,对$\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}$的两边平方即可求出${\overrightarrow{AC}}^{2}+{\overrightarrow{AB}}^{2}=68$,而对$\overrightarrow{AD}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$的两边平方,即可求出${\overrightarrow{AD}}^{2}$的值,从而求出$|\overrightarrow{AD}|$的值.
解答 解:如图,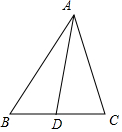 $\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}$;
$\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}$;
∴${\overrightarrow{BC}}^{2}={\overrightarrow{AC}}^{2}-2\overrightarrow{AB}•\overrightarrow{AC}+{\overrightarrow{AB}}^{2}$;
∴$100={\overrightarrow{AC}}^{2}+32+{\overrightarrow{AB}}^{2}$;
∴${\overrightarrow{AC}}^{2}+{\overrightarrow{AB}}^{2}=68$;
又$\overrightarrow{AD}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$;
∴${\overrightarrow{AD}}^{2}=\frac{1}{4}({\overrightarrow{AB}}^{2}+2\overrightarrow{AB}•\overrightarrow{AC}+{\overrightarrow{AC}}^{2})$=$\frac{1}{4}×(68-32)=9$;
∴$|\overrightarrow{AD}|=3$.
故选B.
点评 考查向量减法的几何意义,向量加法的平行四边形法则,以及向量数量积的运算.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{5}$=1 | B. | $\frac{{x}^{2}}{13}$-$\frac{{y}^{2}}{13}$=1 | C. | $\frac{{y}^{2}}{5}$-$\frac{{x}^{2}}{5}$=1 | D. | $\frac{{y}^{2}}{13}$-$\frac{{x}^{2}}{13}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\sqrt{3}$(x+4) | B. | y=$\frac{\sqrt{3}}{3}$(x+4) | C. | y=$\frac{\sqrt{2}}{2}$(x+4) | D. | y=$\sqrt{2}$(x+4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
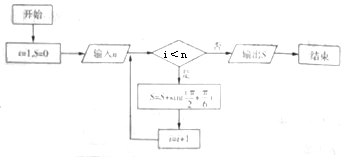
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 0 | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 5 | C. | 7 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com