练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数，其中．

    （1）若函数在上是增函数，求的取值范围．

    （2）若存在，使得关于的方程有三个不相同的实数解，求实数的取值范围．

    【答案】（1）；（2）.

    【解析】

    （1）把函数写成分段函数的形式，再利用分段函数的单调性得不等式组，解不等式组，即可求的取值范围．

    （2）将分和两种情况分类讨论，求出函数单调区间，从而得到关于的不等式，再将问题转化为有解问题，即可得答案．

    （1），

    由在上是增函数，则，解得：，

    ∴的取值范围为：.

    （2）①当时，在上是增函数，

    关于的方程不可能有三个不相等的实数解．

    ②当时，由（1）知在，和，上分别是增函数，

    在，上是减函数，

    当且仅当，即时，方程有三个不相等的实数解．

    即，在，有解，

    令，在，时是增函数，则，

    ∴．

    实数的取值范围是．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设函数.

    （1）当时，求函数的极值；

    （2）若关于的方程有唯一解，且，，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分12分）在△中，角所对的边分别为，已知，，．

    （1）求的值；

    （2）求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

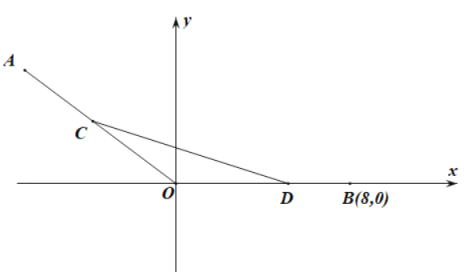
    【题目】如图，在平面直角坐标系中，已知点，点，、分别为线段、上的动点，且满足.

    （1）若，求点的坐标；

    （2）设点的坐标为，求的外接圆的一般方程，并求的外接圆所过定点的坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝.如图所示的弦图中，由四个全等的直角三角形和一个正方形构成．现有五种不同的颜色可供涂色，要求相邻的区域不能用同一种颜色，则不同的涂色方案有（ ）

    A.180B.192C.420D.480

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某旅游爱好者计划从3个亚洲国家A1，A2，A3和3个欧洲国家B1，B2，B3中选择2个国家去旅游.

    (1)若从这6个国家中任选2个，求这2个国家都是亚洲国家的概率；

    (2)若从亚洲国家和欧洲国家中各选1个，求这两个国家包括A1，但不包括B1的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的长轴长为6，且椭圆与圆的公共弦长为．

    （1）求椭圆的方程；

    （2）过点P（0，1）作斜率为的直线与椭圆交于两点，，试判断在轴上是否存在点，使得为以为底边的等腰三角形，若存在，求出点的横坐标的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数是单调递增函数，其反函数是．

    （1）若，求并写出定义域；

    （2）对于⑴的和，设任意，，，求证：；

    （3）已知函数和的图象有交点，求证：它们的交点一定在直线上．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x2ax3（a＞0），x∈R.若对任意的x1∈（2，+∞），都存在x2∈（1，+∞），使得f（x1）f（x2）=1，则a的取值范围是_____.

    查看答案和解析>>

    同步练习册答案