
分析 (1)由短轴和准线方程求出b和a的值,据焦点在x轴上写出椭圆的方程.
(2)分切点为椭圆长轴两个顶点和不是椭圆长轴两个顶点,当切点不过椭圆长轴两个顶点时,设出切线方程y=kx+m,联立切线方程和椭圆方程,由判别式等于0得到k与m的关系,再求出FQ所在直线方程,联立两直线方程求得Q的坐标,由两点间的距离公式可得|OQ|为定值2.
解答 (1)解:由题意知,$\left\{\begin{array}{l}{c=1}\\{\frac{1}{4{a}^{2}}+\frac{45}{16{b}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a2=4,b2=3,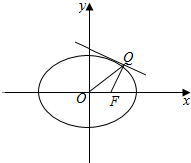
∴椭圆的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)证明:当直线l过椭圆长轴两个顶点时,Q与顶点重合,此时|OQ|=2;
当直线l不过椭圆长轴两个顶点时,设切线方程为y=kx+m,
联立$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得(3+4k2)x2+8kmx+4m2-12=0.
由△=(8km)2-4(3+4k2)(4m2-12)=0,得m2=4k2+3.
∵F(1,0),且FQ⊥l,
∴FQ所在直线方程为y=$-\frac{1}{k}(x-1)$,
联立$\left\{\begin{array}{l}{y=kx+m}\\{y=-\frac{1}{k}(x-1)}\end{array}\right.$,解得Q($\frac{1-km}{1+{k}^{2}},\frac{k+m}{1+{k}^{2}}$),
∴|OQ|=$\sqrt{(\frac{1-km}{1+{k}^{2}})^{2}+(\frac{k+m}{1+{k}^{2}})^{2}}$=$\sqrt{\frac{1-2km+{k}^{2}{m}^{2}+{k}^{2}+2km+{m}^{2}}{(1+{k}^{2})^{2}}}$
=$\sqrt{\frac{(1+{k}^{2})(1+{m}^{2})}{(1+{k}^{2})^{2}}}=\sqrt{\frac{1+{m}^{2}}{1+{k}^{2}}}$=$\sqrt{\frac{4{k}^{2}+4}{1+{k}^{2}}}=2$.
故|OQ|为定值2.
点评 本题考查椭圆的方程、直线和圆的位置关系的应用,考查计算能力,是中档题.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,某机械转动的三个齿轮啮合传动.若A轮的直径为180mm,B、C两轮的直径都是120mm,且∠ABC=70°,求A、C两齿轮的中心距离(精确到1mm).
如图所示,某机械转动的三个齿轮啮合传动.若A轮的直径为180mm,B、C两轮的直径都是120mm,且∠ABC=70°,求A、C两齿轮的中心距离(精确到1mm).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com