练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设四点均在双曲线的右支上.

    （1）若（实数），证明：（O是坐标原点）；

    （2）若，P是线段AB的中点，过点P分别作该双曲线的两条渐近线的垂线，垂足为M、N，求四边形的面积的最大值.

    【答案】（1）见解析（2）1

    【解析】

    （1）由，得

    当直线AB的倾斜角为90°时，设其方程为设，则，且点满足 同理=1，则.

    设直线AB的方程为

    联立方程得整理为

    ①

    故 ②

    ③

    则 由，知直线AB与直线CD的斜率相等.同理， 所以，.

    （2）由，平方得

    将式②、③代入得 ④

    由，知，而使方程①的判别式成立.设于是，

    ， ⑤

    . ⑥

    因为双曲线的两条渐近线相互垂直，所以，四边形是矩形，其面积S等于点P到渐近线距离的乘积.于是，将式⑤、⑥代入上式得由式④得又，则，即直线AB的斜率存在时，所求四边形的面积

    当直线AB斜率不存在时，由，知点，则四边形的面积

    综上，四边形面积的最大值为1.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】命题方程表示双曲线；命题不等式的解集是. 为假， 为真，求的取值范围.

    【答案】

    【解析】试题分析：由命题方程表示双曲线，求出的取值范围，由命题不等式的解集是，求出的取值范围，由为假， 为真，得出一真一假，分两种情况即可得出的取值范围.

    试题解析：

    真

    ，

    真 或

    ∴

    真假

    假真

    ∴范围为

    【题型】解答题
    【结束】
    18

    【题目】如图，设是圆上的动点，点是在轴上的投影， 为上一点，且.

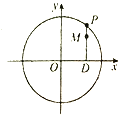
    （1）当在圆上运动时，求点的轨迹的方程；

    （2）求过点且斜率为的直线被所截线段的长度.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在长方体中，底面是边长为的正方形，对角线与相交于点，点在线段上，且，与底面所成角为.

    （1）求证：；

    （2）求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】四棱锥A－BCDE中，底面BCDE为矩形，侧面ABC⊥底面BCDE，侧面ABE⊥底面BCDE，BC＝2，CD＝4。

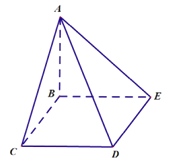
    （I）证明：AB⊥面BCDE；

    （II）若AD＝2，求二面角C－AD－E的正弦值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(本小题满分10分)[选修4-4,极坐标与参数方程选讲]

    在直角坐标系x0y中,曲线C1的参数方程为(为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为p=4sin9

    (1)求曲线C1的普通方程和C2的直角坐标方程;

    (Ⅱ)已知曲线C3的极坐标方程为=α,(0<α<x,p∈R),点A是曲线C3与C1的交点,点B是曲线C3与C2的交点,且A,B均异于原点O,且|AB|=4,求实数α的值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，三棱柱的各棱长均为2， 面，E，F分别为棱的中点．

    （1）求证：直线BE∥平面；

    （2）平面与直线AB交于点M，指出点M的位置，说明理由，并求三棱锥的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】假设某市2011年新建住房400万m2，其中250万m2是中低价房，预计在今后的若干年内，该市每年新建住房面积平均比上一年增长8%．另外，每年新建住房中，中低价房的面积比上一年增加50万m2，那么到哪一年底，

    （1）该市历年所建中低价房的累计面积（以2011年为累计的第一年）将首次不少于4750万m2？

    （2）当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知首项为的等比数列不是递减数列，其前n项和为，且成等差数列。

    （1）求数列的通项公式；

    （2）设，求数列的最大项的值与最小项的值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）当时，求的单调区间；

    （2）若有两个零点，求实数的取值范围.

    查看答案和解析>>

    同步练习册答案