
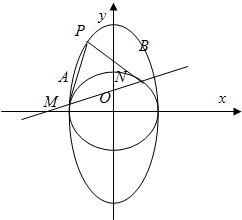 �����⣺��ͼ������ԲC��
�����⣺��ͼ������ԲC��| y2 |
| a2 |
| x2 |
| b2 |
| a2 |
| |OM|2 |
| b2 |
| |ON|2 |
| 25 |
| 16 |
| 16 |
| x0 |
| 16 |
| y0 |
| a2 |
| |OM|2 |
| b2 |
| |ON|2 |
| 25 |
| 16 |
| a2x02 |
| 162 |
| y02 |
| 16 |
| 25 |
| 16 |
| 2 |
| b2(a2-2b2) |
| a2-b2 |
| a2b2 |
| a2-b2 |
| 16 |
| x0 |
| 16 |
| y0 |
| a2 |
| |OM|2 |
| b2 |
| |ON|2 |
| 25 |
| 16 |
| a2x02 |
| 162 |
| y02 |
| 16 |
| 25 |
| 16 |
| y02 |
| a2 |
| x02 |
| 16 |
| x02 |
| 16 |
| y2 |
| 25 |
| x2 |
| 16 |
| 2 |
| b2(a2-2b2) |
| a2-b2 |
| a2b2 |
| a2-b2 |
| 2 |
| 2 |


 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 �����⣺
�����⣺
|
|
| 12 |
| 3cos2��+4sin2�� |
|
| x |
| yz |
| y |
| zx |
| z |
| xy |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
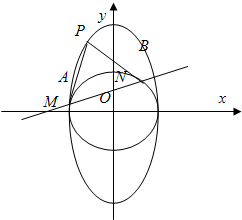 �����⣺��ͼ������ԲC��
�����⣺��ͼ������ԲC��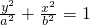 ��a��b��0����һ����P��Բx2+y2=b2����������PA��PB��A��BΪ�е㣩��ֱ��AB��x�ᡢy��ֱ���M��N���㣮
��a��b��0����һ����P��Բx2+y2=b2����������PA��PB��A��BΪ�е㣩��ֱ��AB��x�ᡢy��ֱ���M��N���㣮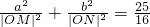 ������ԲC�ķ��̣�
������ԲC�ķ��̣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2010�꽭��ʡ̩�ݸ���ѧ�߿���ѧģ���Ծ��������棩 ���ͣ������
 =M
=M �����������M��
�����������M�� ����F1��F2Ϊ�����ҽ��㣬ֱ��l�IJ�������Ϊ
����F1��F2Ϊ�����ҽ��㣬ֱ��l�IJ�������Ϊ ��tΪ������t��R�������F1��F2��ֱ��l�ľ���֮�ͣ�
��tΪ������t��R�������F1��F2��ֱ��l�ľ���֮�ͣ� ��
��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com