
【题目】一片森林原面积为![]() ,计划从某年开始,每年砍伐一些树林,且每年砍伐面积与上一年剩余面积的百分比相等.并计划砍伐到原面积的一半时,所用时间是10年.为保护生态环境,森林面积至少要保留原面积的
,计划从某年开始,每年砍伐一些树林,且每年砍伐面积与上一年剩余面积的百分比相等.并计划砍伐到原面积的一半时,所用时间是10年.为保护生态环境,森林面积至少要保留原面积的![]() .已知到今年为止,森林剩余面积为原面积的
.已知到今年为止,森林剩余面积为原面积的![]() .
.
(1)求每年砍伐面积与上一年剩余面积的百分比;
(2)到今年为止,该森林已砍伐了多少年?
(3)为保护生态环境,今后最多还能砍伐多少年?
【答案】(1)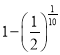 ;(2)5年;(3)15年
;(2)5年;(3)15年
【解析】
(1)根据每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,设每年砍伐面积的百分比为![]() 可建立方程,解之即可得到每年砍伐面积的百分比;
可建立方程,解之即可得到每年砍伐面积的百分比;
(2)设经过![]() 年剩余面积为原来的
年剩余面积为原来的![]() ,根据题意:到今年为止,森林剩余面积为原来的
,根据题意:到今年为止,森林剩余面积为原来的![]() ,可列出关于
,可列出关于![]() 的等式,解之即可;
的等式,解之即可;
(3)根据题意设从今年开始,以后砍了![]() 年,再求出砍伐
年,再求出砍伐![]() 年后剩余面积,由题意,建立关于
年后剩余面积,由题意,建立关于![]() 的不等关系,利用一些不等关系即可求得今后最多还能砍伐多少年
的不等关系,利用一些不等关系即可求得今后最多还能砍伐多少年
(1)设每年降低百分比为![]() .
.
则![]() ,即
,即![]() ,
,
解得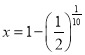 ;
;
(2)设经过![]() 年剩余面积为原面积的
年剩余面积为原面积的![]() ,
,
则![]() ,即
,即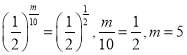 .
.
到今年为止,已砍伐了5年;
(3)设从今年开始,以后砍伐了![]() 年,则
年,则![]() 年后剩余面积为
年后剩余面积为![]() .
.
令![]() ,即
,即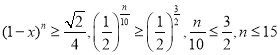 .
.
故今后最多还能砍伐15年.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某乐园按时段收费,收费标准为:每玩一次不超过![]() 小时收费10元,超过
小时收费10元,超过![]() 小时的部分每小时收费
小时的部分每小时收费![]() 元(不足
元(不足![]() 小时的部分按
小时的部分按![]() 小时计算).现有甲、乙二人参与但都不超过
小时计算).现有甲、乙二人参与但都不超过![]() 小时,甲、乙二人在每个时段离场是等可能的。为吸引顾客,每个顾客可以参加一次抽奖活动。
小时,甲、乙二人在每个时段离场是等可能的。为吸引顾客,每个顾客可以参加一次抽奖活动。
(1) 用![]() 表示甲乙玩都不超过
表示甲乙玩都不超过![]() 小时的付费情况,求甲、乙二人付费之和为44元的概率;
小时的付费情况,求甲、乙二人付费之和为44元的概率;
(2)抽奖活动的规则是:顾客通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数![]() ,并按如右所示的程序框图执行.若电脑显示“中奖”,则该顾客中奖;若电脑显示“谢谢”,则不中奖,求顾客中奖的概率.
,并按如右所示的程序框图执行.若电脑显示“中奖”,则该顾客中奖;若电脑显示“谢谢”,则不中奖,求顾客中奖的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①正切函数图象的对称中心是唯一的;
②若函数![]() 的图像关于直线
的图像关于直线![]() 对称,则这样的函数
对称,则这样的函数![]() 是不唯一的;
是不唯一的;
③若![]() ,
,![]() 是第一象限角,且
是第一象限角,且![]() ,则
,则![]() ;
;
④若![]() 是定义在
是定义在![]() 上的奇函数,它的最小正周期是
上的奇函数,它的最小正周期是![]() ,则
,则![]() .
.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC—A1B1C1中,∠ACB=90°,AC=2,BC=CC1=![]() ,P是BC1上一动点,则A1P+PC的最小值为_________.
,P是BC1上一动点,则A1P+PC的最小值为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为偶函数,且函数
为偶函数,且函数![]() 图像的两相邻对称轴间的距离为
图像的两相邻对称轴间的距离为![]() .
.
(1)求![]() ,
,![]() 及
及![]() 的值.
的值.
(2)将函数![]() 的图像向右平移
的图像向右平移![]() 个单位,再将得到的图像上每个点的横坐标伸长到原来的
个单位,再将得到的图像上每个点的横坐标伸长到原来的![]() 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数![]() 的图像,求
的图像,求![]() 的单调递减区间.
的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x-m|-|2x+3m|(m>0).
(1)当m=1时,求不等式f(x)≥1的解集;
(2)对于任意实数x,t,不等式f(x)<|2+t|+|t-1|恒成立,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com