
 表示学生掌握和接受概念的能力, x表示讲授概念的时间(单位:min),可有以下的关系:
表示学生掌握和接受概念的能力, x表示讲授概念的时间(单位:min),可有以下的关系:

 ,关键是从图象上知道6<x<
,关键是从图象上知道6<x<
 -6=
-6= ,其实就是持续的时间,最后和10分钟比较大小即可.
,其实就是持续的时间,最后和10分钟比较大小即可. 2分
2分 开讲后第5min比开讲后第20min,学生接受能力强一些. 3分
开讲后第5min比开讲后第20min,学生接受能力强一些. 3分 时,
时, 4分
4分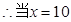 时
时  5分
5分 时,
时, 6分
6分 开讲后10mim(包括10mim)学生接受能力最强,能维持6min.7分
开讲后10mim(包括10mim)学生接受能力最强,能维持6min.7分 9分
9分 , 11分
, 11分
 老师不能在学生一直达到所需接受能力的的状态下讲授完这个新概念12分
老师不能在学生一直达到所需接受能力的的状态下讲授完这个新概念12分

 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源:不详 题型:解答题
 (
( ).
). 时,
时,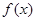 在
在 上是减函数,在
上是减函数,在 上是增函数,并写出当
上是增函数,并写出当 时
时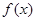 的单调区间;
的单调区间;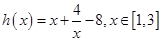 ,函数
,函数 ,若对任意
,若对任意 ,总存在
,总存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 立方米,只付基本费10元加上定额损耗费2元;
立方米,只付基本费10元加上定额损耗费2元; 立方米时,除了付以上同样的基本费和定额损耗费外,超过部分每立方米加付
立方米时,除了付以上同样的基本费和定额损耗费外,超过部分每立方米加付 元的超额费.
元的超额费. (元)与用水量
(元)与用水量 (立方米)的函数关系式;
(立方米)的函数关系式;| 月份 | 用水量(立方米) | 水费(元) |
| 一 | 5 | 17 |
| 二 | 6 | 22 |
| 三 |  | 12 |
 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,g(x)=-x2+bx,若y=f(x)的图象与y=g(x)的图象有且仅有两个不同的公共点A(x1,y1),B(x2,y2),则下列判断正确的是 ( ).
,g(x)=-x2+bx,若y=f(x)的图象与y=g(x)的图象有且仅有两个不同的公共点A(x1,y1),B(x2,y2),则下列判断正确的是 ( ).| A.x1+x2>0,y1+y2>0 |
| B.x1+x2<0,y1+y2>0 |
| C.x1+x2>0,y1+y2<0 |
| D.x1+x2<0,y1+y2<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com