
����Ŀ��ij�̳����й���齱����齱���з��г���Ų�ͬ�⣬�������ͬ��20��С����20��С���ŵľ�Ҷͼ��ͼ��ʾ����������£��ӳ齱���������ȡһ������ȡ��С������ʮλ����Ϊl����������Ϊһ�Ƚ�������100Ԫ������ȡ��С������ʮλ����Ϊ2����������Ϊ���Ƚ�������50Ԫ������ȡ��С�������������н�����ij�˿��зŻصij齱���Σ����γ齱������� ��I����ù˿������γ齱��ǡ��һ���н��ĸ��ʣ�
���Ǹù˿����γ齱��Ľ���֮��Ϊ�������X����X�ķֲ��к���ѧ������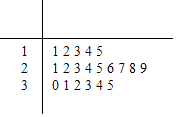
���𰸡��⣺������һ�γ齱����i�Ƚ��ĸ���ΪPi��i=1��2����û���н��ĸ���ΪP0 �� ��P1+P2= ![]() =
= ![]() �����н��ĸ���Ϊ
�����н��ĸ���Ϊ ![]() ��
��
��ù˿����γ齱��ǡ��һ���н��ĸ���Ϊ��
P= ![]() =
= ![]() ��
��
����X�Ŀ���ȡֵΪ0��50��100��150��200��
P��X=0��= ![]() ��
��
P��X=50��= ![]() =
= ![]() ��
��
P��X=100��= ![]() =
= ![]() ��
��
P��X=150��= ![]() =
= ![]() ��
��
P��X=200��= ![]() =
= ![]() ��
��
��X�ķֲ���Ϊ��
X | 0 | 50 | 100 | 150 | 200 |
P |
|
|
|
|
|
��EX= ![]() =55��Ԫ��
=55��Ԫ��
��������������һ�γ齱����i�Ƚ��ĸ���ΪPi��i=1��2����û���н��ĸ���ΪP0 �� �ɴ�������ù˿����γ齱��ǡ��һ���н��ĸ��ʣ�����X�Ŀ���ȡֵΪ0��50��100��150��200���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к�EX��
�����㾫�����������⣬������Ҫ�˽⾥Ҷͼ(��Ҷͼ�ֳơ�֦Ҷͼ��������˼·�ǽ������е�����λ�����бȽϣ������Ĵ�С���������仯�����λ��Ϊһ�����ɣ����������仯���λ������Ϊ��֦��Ҷ�����������ɵĺ��棬�����Ϳ�������ؿ���ÿ�����ɺ��漸������ÿ���������Ƕ���)����Ҫ������ɢ�������������ֲ���(���������Ʒ����������У������������X����ȡ��ֵ�����ǿ���һ������һһ�г����������������������ɢ�������������ɢ����������ķֲ��У�һ���,����ɢ���������X����ȡ��ֵΪx1,x2,.....,xi,......,xn��Xȡÿһ��ֵ xi(i=1,2,......���ĸ���P(��=xi����Pi����Ʊ�Ϊ��ɢ���������X �ĸ��ʷֲ�����Ʒֲ���)�����֪ʶ���Ǵ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����н�����ȷ���ǣ� ��
A.�����涼�������εļ�����������
B.һƽ���һ���õ�һ������һ����̨
C.���IJ��ⳤ��������εı߳���ȣ������������������
D.Բ�Ķ��������Բ���ϵ�����һ������߶���ĸ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������R�ϵ�ż����f��x������f��x+1��= ![]() ����f��x����[��3����2]���Ǽ�������������������������ε������ڽǣ��� ��
����f��x����[��3����2]���Ǽ�������������������������ε������ڽǣ��� ��
A.f��sin������f��sin�£�
B.f��cos������f��cos�£�
C.f��sin������f��cos�£�
D.f��sin������f��cos�£�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() ��g��x��=f��x����a
��g��x��=f��x����a
��1����a=2ʱ������g��x������㣻
��2��������g��x�����ĸ���㣬��a��ȡֵ��Χ��
��3���ڣ�2���������£���g��x�����ĸ����ֱ�Ϊx1 �� x2 �� x3 �� x4 �� ��x1+x2+x3+x4��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ں���f1��x����f2��x����h��x�����������ʵ��a��bʹ��h��x��=af1��x��+bf2��x������ô��h��x��Ϊf1��x����f2��x�������ɺ�����
��1���������� ![]() ��h��x���Ƿ�Ϊf1��x���� f2��x�������ɺ�������˵�����ɣ�
��h��x���Ƿ�Ϊf1��x���� f2��x�������ɺ�������˵�����ɣ�
��2���� ![]() �����ɺ���h��x����������ʽ3h2��x��+2h��x��+t��0��x��[2��4]�Ϻ��������ʵ��t��ȡֵ��Χ��
�����ɺ���h��x����������ʽ3h2��x��+2h��x��+t��0��x��[2��4]�Ϻ��������ʵ��t��ȡֵ��Χ��
��3���� ![]() ��ȡa��0��b��0�����ɺ���h��x��ͼ�����͵�����Ϊ��2��8����������������ʵ��x1 �� x2��x1+x2=1�������Ƿ�������ij���m��ʹh��x1��h��x2����m�������������ڣ�������m��ֵ����������ڣ���˵�����ɣ�
��ȡa��0��b��0�����ɺ���h��x��ͼ�����͵�����Ϊ��2��8����������������ʵ��x1 �� x2��x1+x2=1�������Ƿ�������ij���m��ʹh��x1��h��x2����m�������������ڣ�������m��ֵ����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʵ��a��b���������㡰*���� ![]() ����f��x��=��2x��1��*��x��1�����ҹ���x�ķ���Ϊf��x��=m��m��R��ǡ������������ȵ�ʵ����x1 �� x2 �� x3 �� ��ʵ��m��ȡֵ��Χ����x1+x2+x3��ȡֵ��Χ�� ��
����f��x��=��2x��1��*��x��1�����ҹ���x�ķ���Ϊf��x��=m��m��R��ǡ������������ȵ�ʵ����x1 �� x2 �� x3 �� ��ʵ��m��ȡֵ��Χ����x1+x2+x3��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��R������f��x��=����x2+ax��ex �� ��x��R��eΪ��Ȼ�����ĵ�����
��1����a=2ʱ������f��x���ĵ����������䣮
��2������f��x���Ƿ�ΪR�ϵĵ������������ǣ����a��ȡֵ��Χ�������ǣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() x2+2ax��g��x��=3a2lnx+b����������y=f��x����y=g��x���й����㣬���ڸõ㴦��������ͬ����a�ʣ�0��+�ޣ�ʱ��ʵ��b�����ֵ�ǣ� ��
x2+2ax��g��x��=3a2lnx+b����������y=f��x����y=g��x���й����㣬���ڸõ㴦��������ͬ����a�ʣ�0��+�ޣ�ʱ��ʵ��b�����ֵ�ǣ� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com