
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)若![]() 和
和![]() 在
在![]() 有相同的单调区间,求
有相同的单调区间,求![]() 的取值范围;
的取值范围;
(Ⅱ)令![]() (
(![]() ),若
),若![]() 在定义域内有两个不同的极值点.
在定义域内有两个不同的极值点.
(i)求![]() 的取值范围;
的取值范围;
(ii)设两个极值点分别为![]() ,
, ![]() ,证明:
,证明: ![]() .
.
【答案】(Ⅰ)![]() (Ⅱ)(i)
(Ⅱ)(i)![]() (ii)详见解析
(ii)详见解析
【解析】【试题分析】(1)借助题设条件,运用导数与函数的单调性之间的关系分析求解;(2)先依据题设条件将问题进行等价转化,再运用导数知识分析求解:
(Ⅰ)![]() .函数
.函数![]() 的定义域为
的定义域为![]() ,
, ![]() ,
,
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
![]()
![]() 若在
若在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
则![]() .
.
(Ⅱ)(i)依题意,函数![]() 的定义域为
的定义域为![]() ,
, ![]() ,
,
所以方程![]() 在
在![]() 有两个不同根.
有两个不同根.
即方程![]() 在
在![]() 有两个不同根,
有两个不同根,
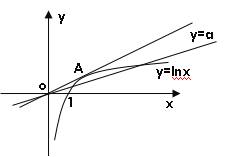
转化为,函数![]() 与函数
与函数![]() 的图象在
的图象在![]() 有两个不同交点,如图.
有两个不同交点,如图.
可见,若令过原点且切于函数![]() 图象的直线斜率为
图象的直线斜率为![]() ,
,
只需![]() .
.
令切点![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() ,
,
解得![]() ,于是
,于是![]() ,所以
,所以![]() .
.
(ii)由(i)可知![]() ,
, ![]() 分别是方程
分别是方程![]() 的两个根,
的两个根,
即![]() ,
, ![]() ,不妨设
,不妨设![]() ,作差得
,作差得![]() ,即
,即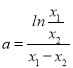 ,
,
原不等式![]() 等价于
等价于![]() ,即
,即![]() ,即
,即![]() ,
,
令![]() ,则
,则![]() ,
, ![]() ,即
,即![]() ,
,
设![]() ,
, ![]() ,
, 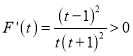 ,
,
∴函数![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() ,即不等式
,即不等式![]() 成立,
成立,
故所证不等式![]() 成立.
成立.


科目:高中数学 来源: 题型:
【题目】(本小题满分12分)在如图所示的五面体中,面![]() 为直角梯形,
为直角梯形, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是边长为2的正三角形.
是边长为2的正三角形.
(1)证明: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(数学(文)卷·2017届湖北省沙市中学高三上学期第七次双周练第16题)埃及数学中有一个独特现象:除![]() 用一个单独的符号表示以外,其它分数都要写成若干个单分数和的形式.例如
用一个单独的符号表示以外,其它分数都要写成若干个单分数和的形式.例如![]() 可以这样理解:假定有两个面包,要平均分给5个人,如果每人
可以这样理解:假定有两个面包,要平均分给5个人,如果每人![]() ,不够,每人
,不够,每人![]() ,余
,余![]() ,再将这
,再将这![]() 分成5份,每人得
分成5份,每人得![]() ,这样每人分得
,这样每人分得![]() .形如
.形如![]() 的分数的分解:
的分数的分解: ![]() ,
, ![]() ,
, ![]() ,按此规律,
,按此规律, ![]() =____________;
=____________; ![]() = ____________
= ____________![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点与其短轴得一个端点是正三角形的三个顶点,点
的左右焦点与其短轴得一个端点是正三角形的三个顶点,点![]() 在椭圆
在椭圆![]() 上,直线
上,直线![]() 与椭圆交于
与椭圆交于![]() 两点,与
两点,与![]() 轴,
轴, ![]() 轴分别相交于点
轴分别相交于点![]() 合点
合点![]() ,且
,且![]() ,点
,点![]() 时点
时点![]() 关于
关于![]() 轴的对称点,
轴的对称点, ![]() 的延长线交椭圆于点
的延长线交椭圆于点![]() ,过点
,过点![]() 分别做
分别做![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() .
.
(1) 求椭圆![]() 的方程;
的方程;
(2)是否存在直线![]() ,使得点
,使得点![]() 平分线段
平分线段![]() ?若存在,请求出直线
?若存在,请求出直线![]() 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() ),以椭圆内一点
),以椭圆内一点![]() 为中点作弦
为中点作弦![]() ,设线段
,设线段![]() 的中垂线与椭圆相交于
的中垂线与椭圆相交于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆的离心率;
(Ⅱ)试判断是否存在这样的![]() ,使得
,使得![]() ,
, ![]() ,
, ![]() ,
, ![]() 在同一个圆上,并说明理由.
在同一个圆上,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
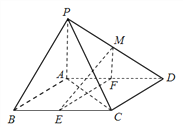
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形, ![]() ,侧面
,侧面![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)如果直线![]() 与平面
与平面![]() 所成的角和直线
所成的角和直线![]() 与平面
与平面![]() 所成的角相等,求
所成的角相等,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市理论预测2010年到2014年人口总数与年份的关系如下表所示
年份2010+x(年) | 0 | 1 | 2 | 3 | 4 |
人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
(1)请根据上表提供的数据,求出y关于x的线性回归方程;
(2) 据此估计2015年该城市人口总数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com