
直角坐标平面上,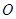 为原点,
为原点,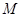 为动点,
为动点,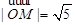 ,
,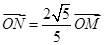 . 过点
. 过点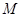 作
作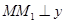 轴于
轴于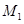 ,过
,过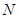 作
作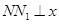 轴于点
轴于点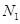 ,
,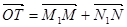 . 记点
. 记点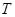 的轨迹为曲线
的轨迹为曲线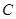 ,
,
点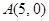 、
、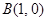 ,过点
,过点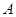 作直线
作直线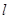 交曲线
交曲线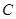 于两个不同的点
于两个不同的点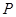 、
、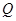 (点
(点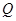 在
在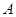 与
与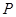 之间).
之间).
(1)求曲线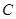 的方程;
的方程;
(2)是否存在直线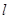 ,使得
,使得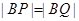 ,并说明理由.
,并说明理由.
(1)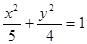 (2)不存在直线l,使得|BP|=|BQ|
(2)不存在直线l,使得|BP|=|BQ|
【解析】
试题分析:(Ⅰ)设点T的坐标为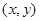 ,点M的坐标为
,点M的坐标为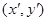 ,则M1的坐标为(0,
,则M1的坐标为(0,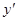 ),
),
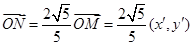 ,于是点N的坐标为
,于是点N的坐标为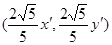 ,N1的坐标
,N1的坐标
为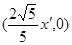 ,所以
,所以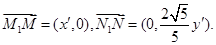
由
由此得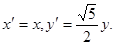
由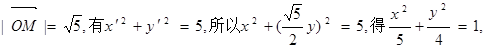
即所求的方程表示的曲线C是椭圆.
(Ⅱ)点A(5,0)在曲线C即椭圆的外部,当直线l的斜率不存在时,直线l与椭圆C
无交点,所以直线l斜率存在,并设为k.
直线l的方程为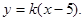
由方程组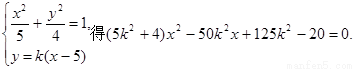
依题意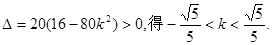
当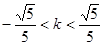 时,设交点
时,设交点 PQ的中点为
PQ的中点为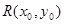 ,
,
则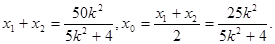
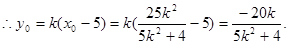
又
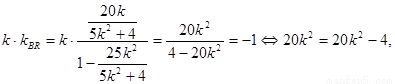
而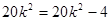 不可能成立,所以不存在直线l,使得|BP|=|BQ|.
不可能成立,所以不存在直线l,使得|BP|=|BQ|.
考点:椭圆的标准方程;直线与圆锥曲线的综合问题.
点评:本题主要考查了椭圆的标准方程和椭圆与直线的关系.当涉及直线与圆锥曲线的位置关系时,常需要把直线方程与圆锥曲线的方程联立,借助韦达定理求得答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源:2002年全国各省市高考模拟试题汇编 题型:013
有四个命题:
①若 是实数,则正整数n的最小值是4
是实数,则正整数n的最小值是4
②设z是虚数,则z+ ∈
∈
③若 都是非零复数,
都是非零复数,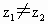 ,且复平面上O为原点,点A和B分别与
,且复平面上O为原点,点A和B分别与 和
和 对应,∠AOB=
对应,∠AOB= ,则
,则
④若复数z满足|z- |≤1,则
|≤1,则 ≤arg(-zi)≤
≤arg(-zi)≤ ,其中真命题是
,其中真命题是
[ ]
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com