
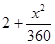 )升,司机的工资是每小时14元.
)升,司机的工资是每小时14元. 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源:不详 题型:解答题
 立方米,只付基本费10元加上定额损耗费2元;
立方米,只付基本费10元加上定额损耗费2元; 立方米时,除了付以上同样的基本费和定额损耗费外,超过部分每立方米加付
立方米时,除了付以上同样的基本费和定额损耗费外,超过部分每立方米加付 元的超额费.
元的超额费. (元)与用水量
(元)与用水量 (立方米)的函数关系式;
(立方米)的函数关系式;| 月份 | 用水量(立方米) | 水费(元) |
| 一 | 5 | 17 |
| 二 | 6 | 22 |
| 三 |  | 12 |
 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 (正常情况
(正常情况 ,且教职工平均月评价分数在50分左右,若有突出贡献可以高于100分)计算当月绩效工资
,且教职工平均月评价分数在50分左右,若有突出贡献可以高于100分)计算当月绩效工资 元.要求绩效工资不低于500元,不设上限且让大部分教职工绩效工资在600元左右,另外绩效工资越低、越高人数要越少.则下列函数最符合要求的是( )
元.要求绩效工资不低于500元,不设上限且让大部分教职工绩效工资在600元左右,另外绩效工资越低、越高人数要越少.则下列函数最符合要求的是( )A. | B. |
C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 为默认值,f(n+1)的值通过执行循环体“f(n+1)=
为默认值,f(n+1)的值通过执行循环体“f(n+1)= ”后计算得出.则f(2)= ;当从入口A输入的正整数n=__ _时,从出口B输出的运算结果是
”后计算得出.则f(2)= ;当从入口A输入的正整数n=__ _时,从出口B输出的运算结果是 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com