
| A. | ($\frac{3}{2}$,+∞) | B. | ($\frac{3}{2}$,$\frac{25}{8}$) | C. | ($\frac{3}{2}$,$\frac{25}{16}$) | D. | ($\frac{2}{3}$,$\frac{3}{4}$) |
分析 由题意求出当x∈[-1,0)时的f(x),把函数g(x)=|f(x)-$\frac{1}{2}$|-mx-m+1在(-1,1]内恰有3个零点,转化为函数y=|f(x)-$\frac{1}{2}$|与y=mx+m-1的图象有三个不同交点.数形结合得答案.
解答 解:当x∈(-1,0)时,x+1∈(0,1),
f(x)=$\frac{1}{f(x+1)}$-1=$\frac{1}{x+1}$-1,
若函数g(x)=|f(x)-$\frac{1}{2}$|-mx-m+1在(-1,1]内恰有3个零点,
即方程|f(x)-$\frac{1}{2}$|-mx-m+1=0在(-1,1]内恰有3个根,
也就是函数y=|f(x)-$\frac{1}{2}$|与y=mx+m-1的图象有三个不同交点.
作出函数图形如图: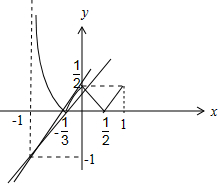
由图可知,过点(-1,-1)与点($-\frac{1}{3}$,0)的直线的斜率为$\frac{3}{2}$;
过点(-1,1),且与曲线y=$\frac{1}{x+1}-1-\frac{1}{2}$=$\frac{-3x-1}{2(x+1)}$相切的切点为(x0,y0),
则$y′{|}_{x={x}_{0}}$=$\frac{-1}{({x}_{0}+1)^{2}}$,
切线方程为y+$\frac{3{x}_{0}+1}{2({x}_{0}+1)}=-\frac{1}{({x}_{0}+1)^{2}}$(x-x0),则切点为($-\frac{1}{5},-\frac{1}{4}$).
∴切线的斜率为k=$\frac{1-\frac{1}{4}}{-1-(-\frac{1}{5})}=-\frac{25}{16}$,由对称性可知,过点(-1,-1)与曲线|f(x)-$\frac{1}{2}$|在(-1,0)上相切的切线的斜率为$\frac{25}{16}$.
∴使函数y=|f(x)-$\frac{1}{2}$|与y=mx+m-1的图象有三个不同交点的m的取值范围为($\frac{3}{2}$,$\frac{25}{16}$).
故选:C.
点评 本题考查函数的零点判定定理,考查数形结合的解题思想方法和数学转化思想方法,训练了利用导数求曲线的切线方程,是中档题.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{21}{2}$ | C. | 6 | D. | 与b值有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{6}$,-2) | B. | ($\frac{π}{12}$,2) | C. | ($-\frac{π}{12}$,-2) | D. | ($-\frac{π}{12}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | -10 | C. | -20 | D. | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com